1.7 — Price Elasticity
ECON 306 • Microeconomic Analysis • Spring 2023
Ryan Safner
Associate Professor of Economics
safner@hood.edu
ryansafner/microS23
microS23.classes.ryansafner.com
Price Elasticity of Demand
Price Elasticity of Demand
- Price elasticity of demand measures how much (in %) quantity demanded changes in response to a (1%) change in price
εqD,p=%ΔqD%Δp

Price Elasticity of Demand: Elastic vs. Inelastic
εqD,p=%ΔqD%Δp
| “Elastic” | “Unit Elastic” | “Inelastic” | |
|---|---|---|---|
| Intuitively: | Large response | Proportionate response | Little response |
| Mathematically: | |εqD,p|>1 | |εqD,p|=1 | |εqD,p|<1 |
| Numerator > Denominator | Numerator = Denominator | Numerator < Denominator | |
| 1% change in p causes | More than 1% change in qD | Exactly 1% change in qD | Less than 1% change in qD |
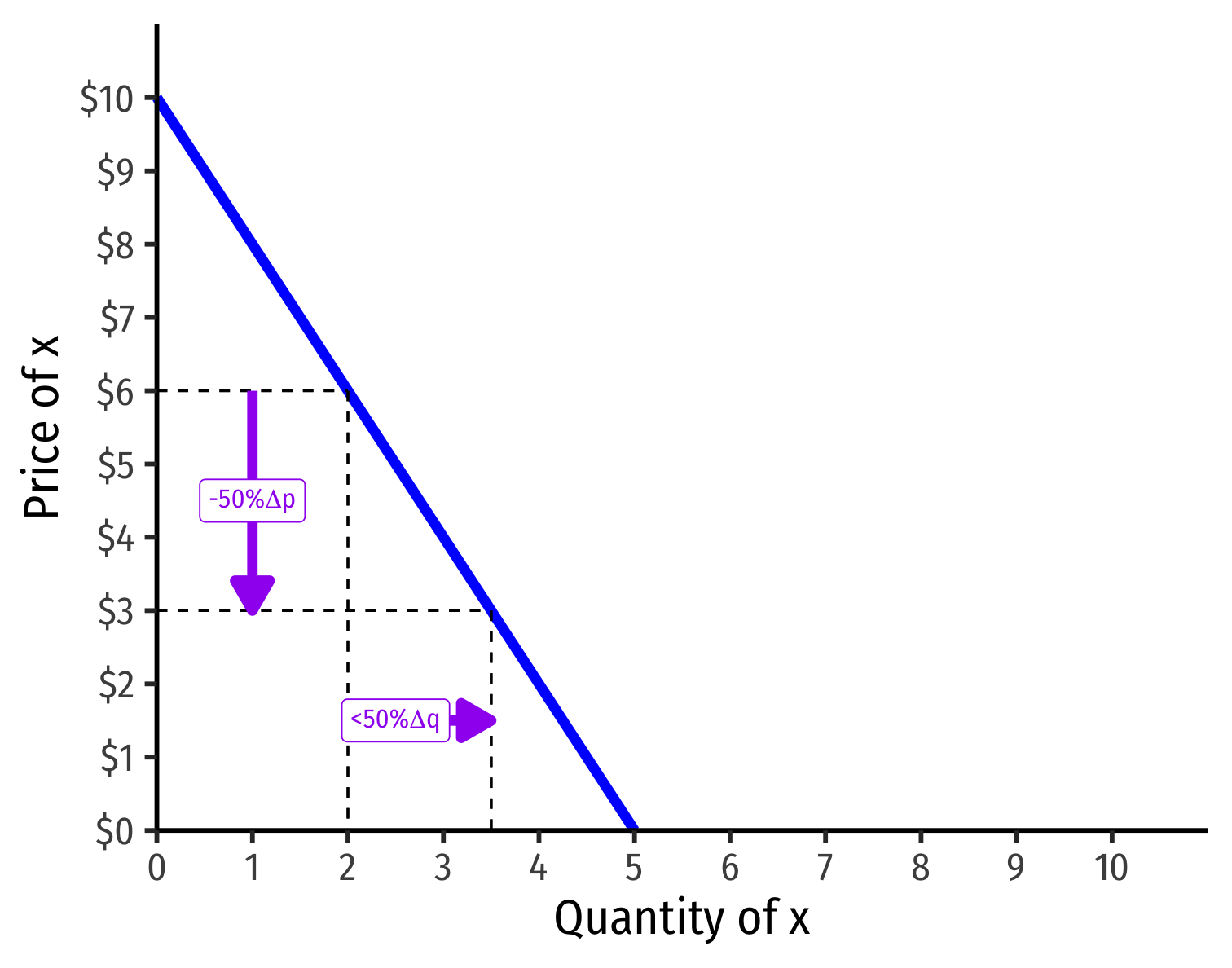
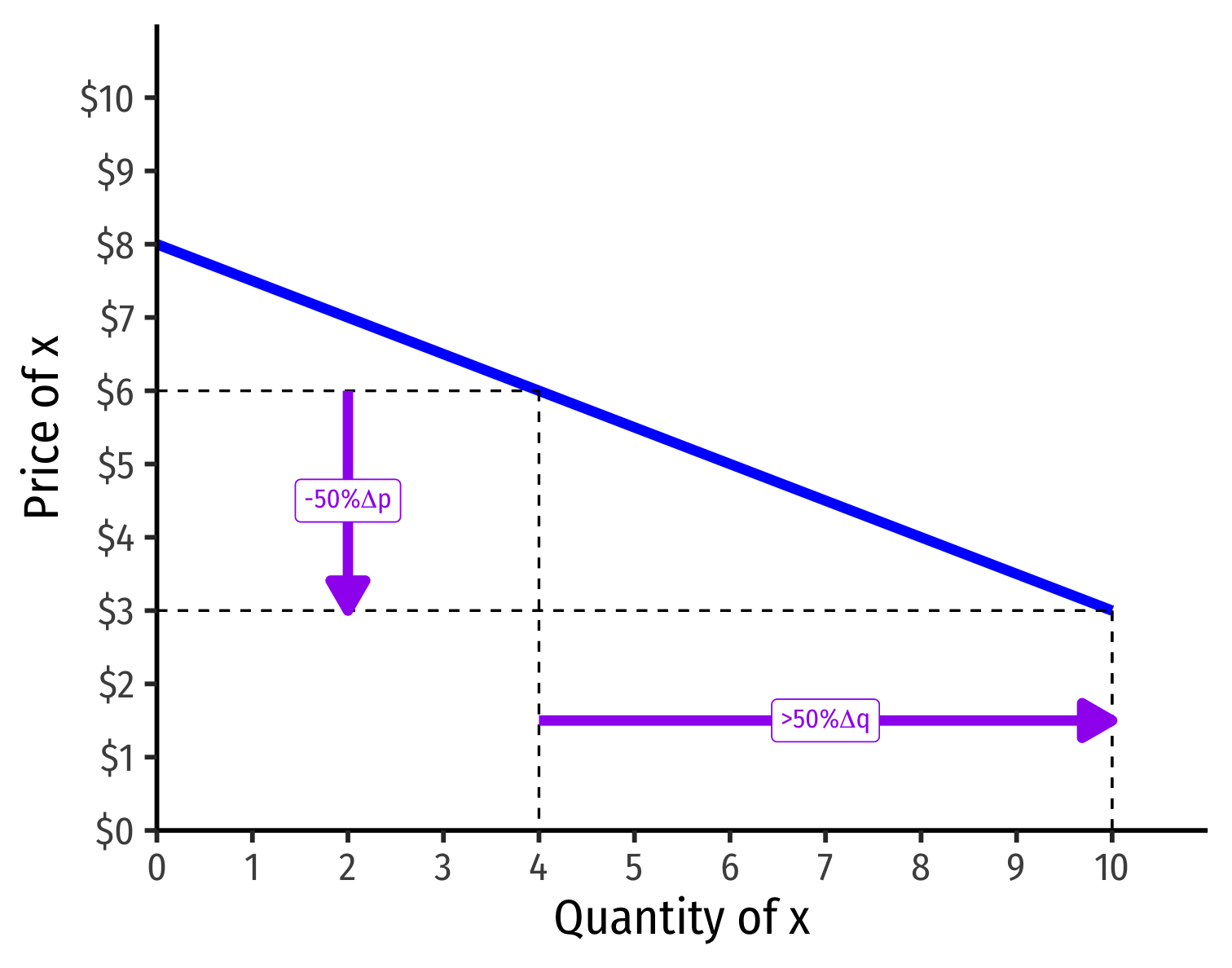
Visualizing Price Elasticity of Demand
An identical 50% price cut on an:
“Inelastic” Demand Curve
“Elastic” Demand Curve
Price Elasticity of Demand Formula
εqD,p=%ΔqD%Δp

Price Elasticity of Demand Formula
εq,p=%Δq%Δp=(Δqq)(Δpp)

Price Elasticity of Demand Formula
εq,p=%Δq%Δp=(Δqq)(Δpp)=ΔqΔp×pq

Price Elasticity of Demand Formula
εq,p=ΔqΔp×pq
First term: direction of the effect
- This is the price effect!
- Always negative!
Second term: magnitude of the effect
- Will change depending on p and q

Price Elasticity of Demand Formula
εq,p=ΔqΔp×pq
You’ve learned “arc”-price elasticity using the “midpoint formula’ between 2 points
Here is a more general formula: the elasticity at any single point!
We can actually simplify this even more...does the first term remind you of anything?

Price Elasticity of Demand Formula
εq,p=1slope×pq
First term is actually the inverse of the slope of the inverse demand curve (that we graph)!
To find the elasticity at any point, we need 3 things:
- The price
- The associated quantity demanded
- The slope of (inverse) demand

Example
Example: The demand for movie tickets in a small town is given by:
q=1000−50p
Find the inverse demand function.
What is the price elasticity of demand at a price of $5.00?
What is the price elasticity of demand at a price of $12.00?
At what price is demand unit elastic (i.e. εq,p=−1)?
Price Elasticity Changes Along the Demand Curve
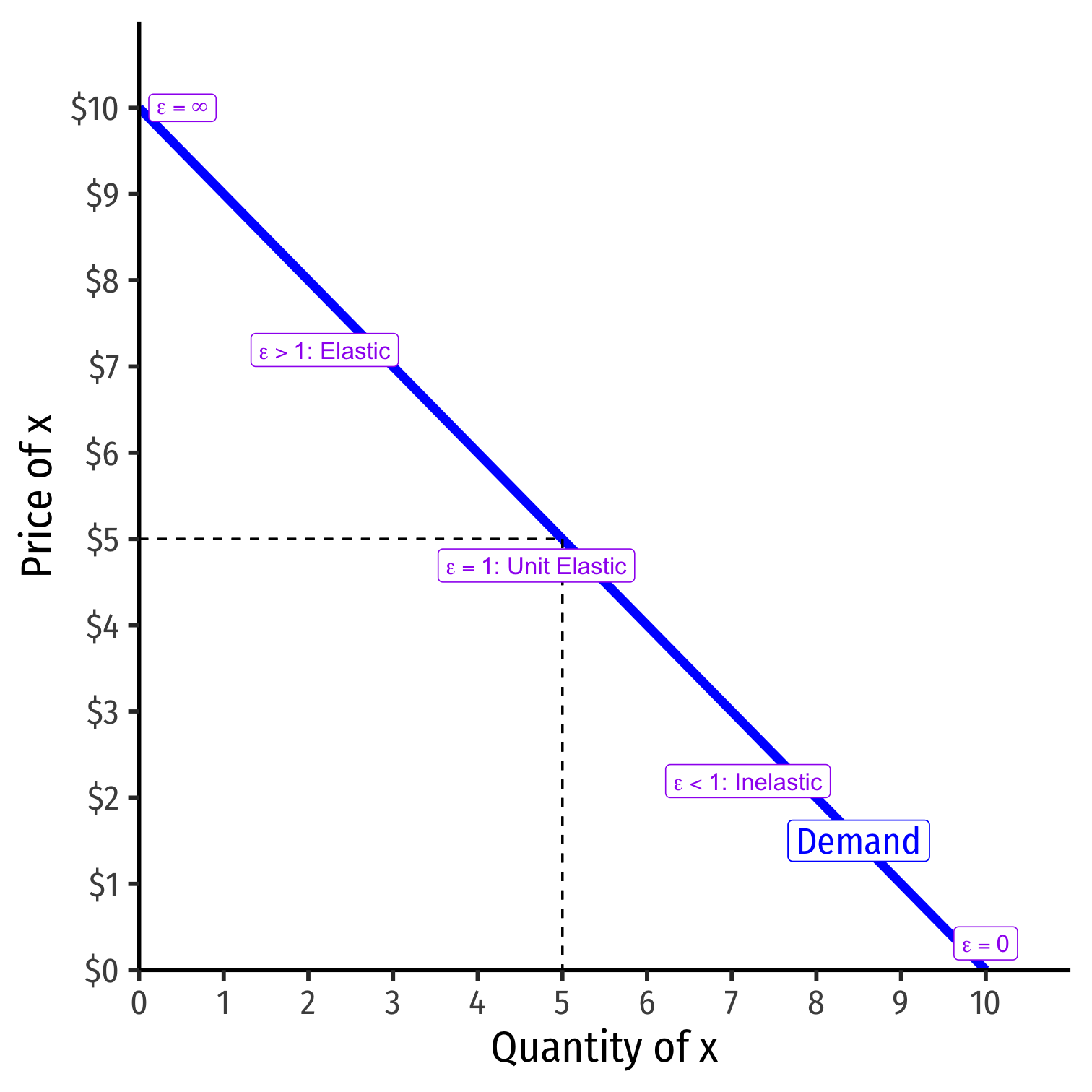
εq,p=1slope×pq
Elasticity ≠ slope (but they are related)!
Price elasticity changes along the demand curve
Gets less elastic as ↓ price (↑ quantity )
- 1slope is constant
- pq gets smaller as ↓p and ↑q
Determinants of Price Elasticity of Demand
What determines how responsive your buying behavior is to a price change?
More (fewer) substitutes ⟹ more (less) elastic
- Larger categories of products (less elastic) vs. specific brand (more elastic)
- Necessities (less elastic) vs. luxuries (more elastic)
- Large (more elastic) vs. small (less elastic) portion of budget
More (less) time to adjust ⟹ more (less) elastic

Price Elasticity of Demand and Revenues
Price Elasticity of Demand and Revenues
- Price elasticity of demand is closely related to Revenues (R)†
R(q)=pq

Price Elasticity of Demand and Revenues
- Price elasticity of demand is closely related to Revenues (R)†
R(q)=pq
| Demand is | ΔR and Δp |
|---|---|
| Elastic |ε|>1 | p & R change opposite |
| Unit Elastic |ε|=1 | R maximized |
| Inelastic |ε|<1 | p & R change together |

Price Elasticity of Demand and Revenues
- Price elasticity of demand is closely related to Revenues (R)†
R(q)=pq
| Demand is | ΔR and Δp |
|---|---|
| Elastic |ε|>1 | p & R change opposite |
| Unit Elastic |ε|=1 | R maximized |
| Inelastic |ε|<1 | p & R change together |

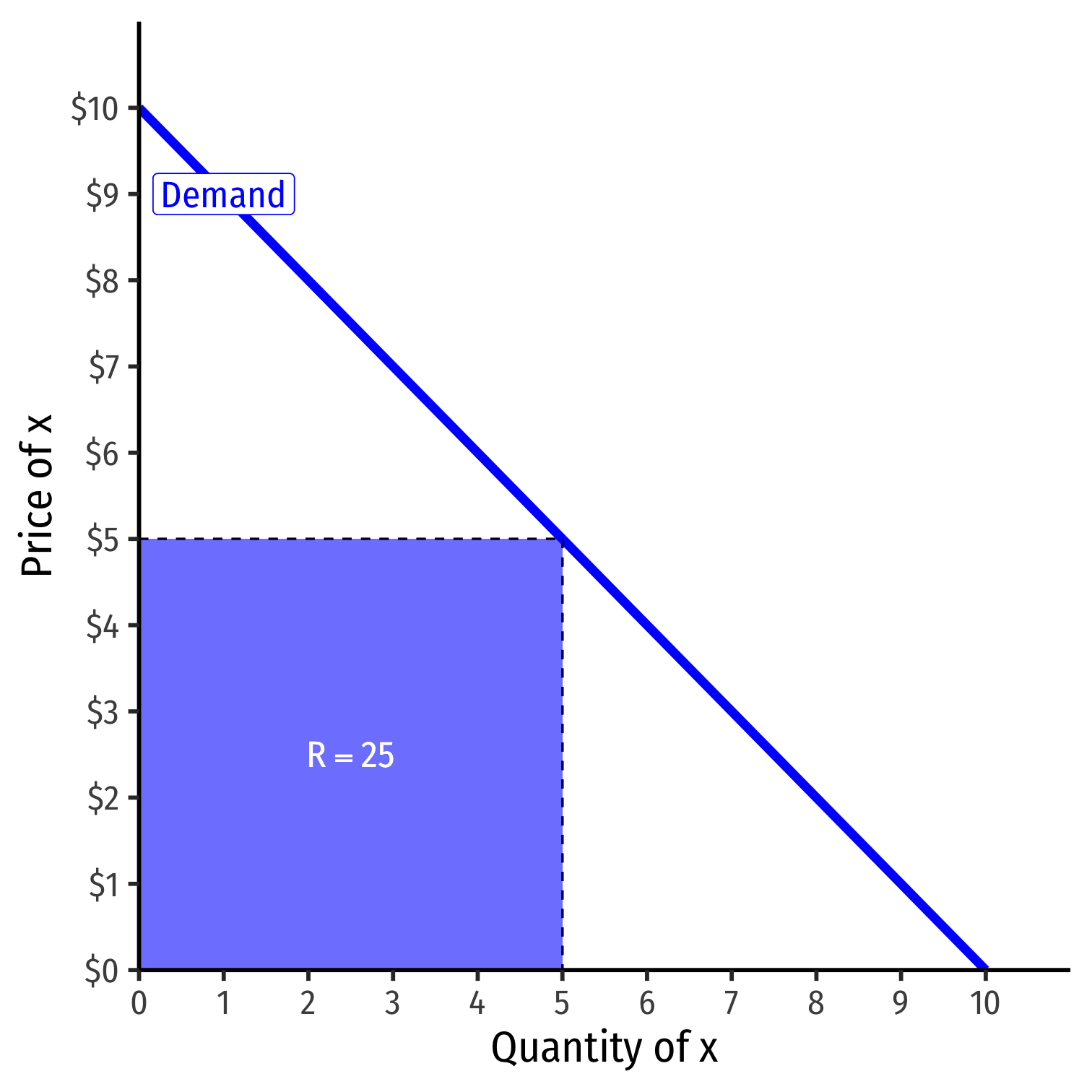
Revenues: Example I
Revenues: Example I
Revenues: Example II
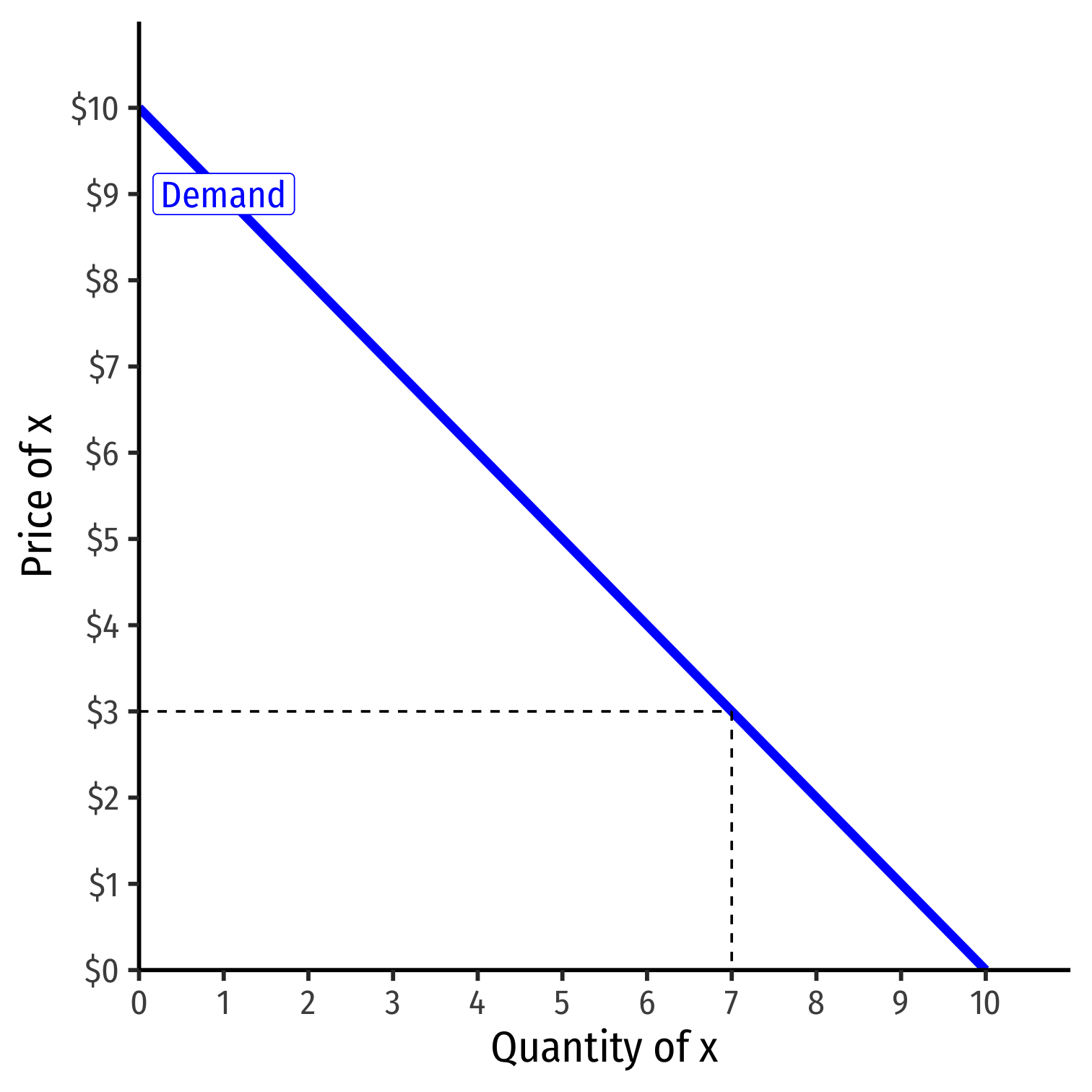
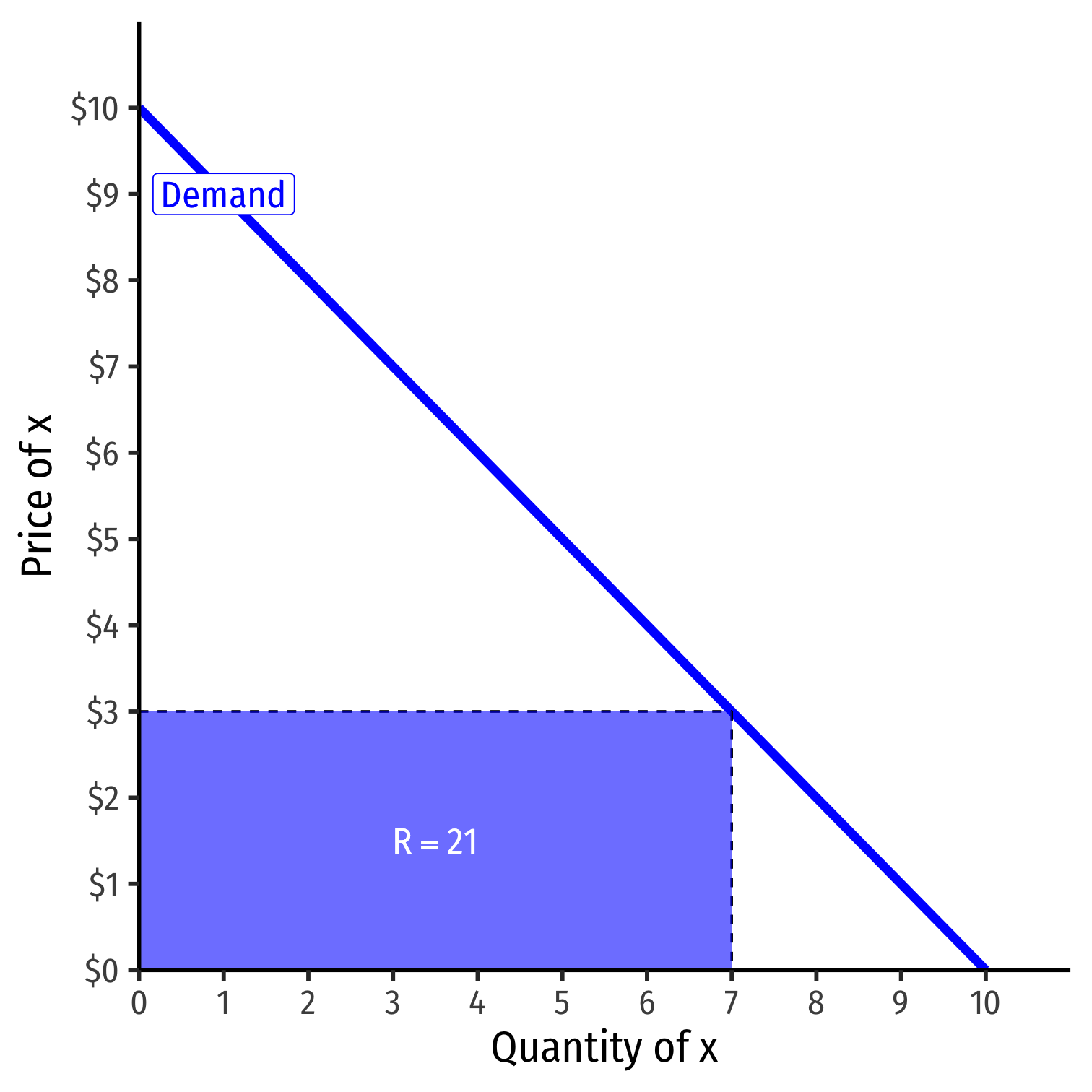
Revenues: Example II
Visualizing Price Elasticity of Demand and Revenues
“Inelastic” Demand Curve
(Agricultural Products)
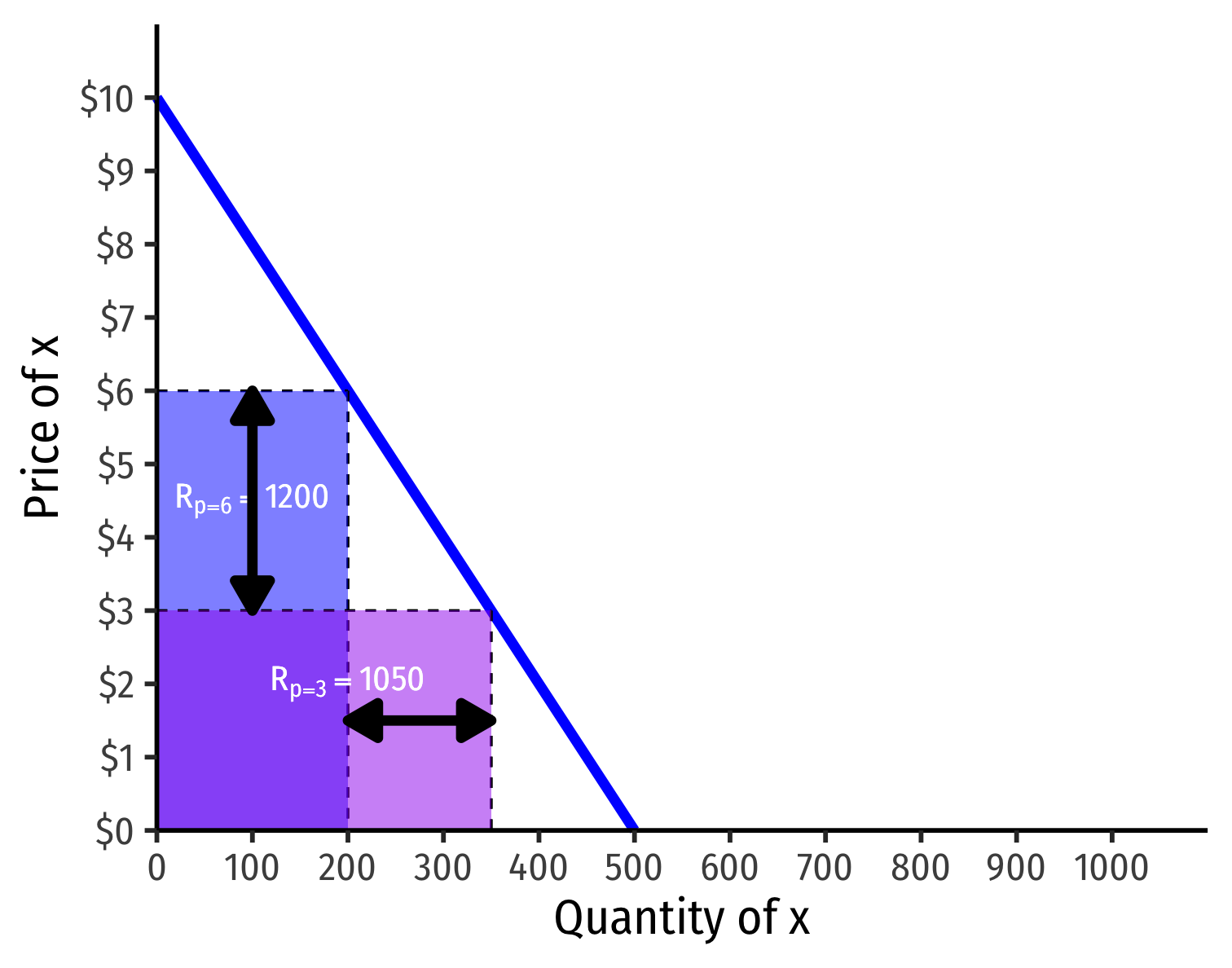
“Elastic” Demand Curve
(Computer Chips)
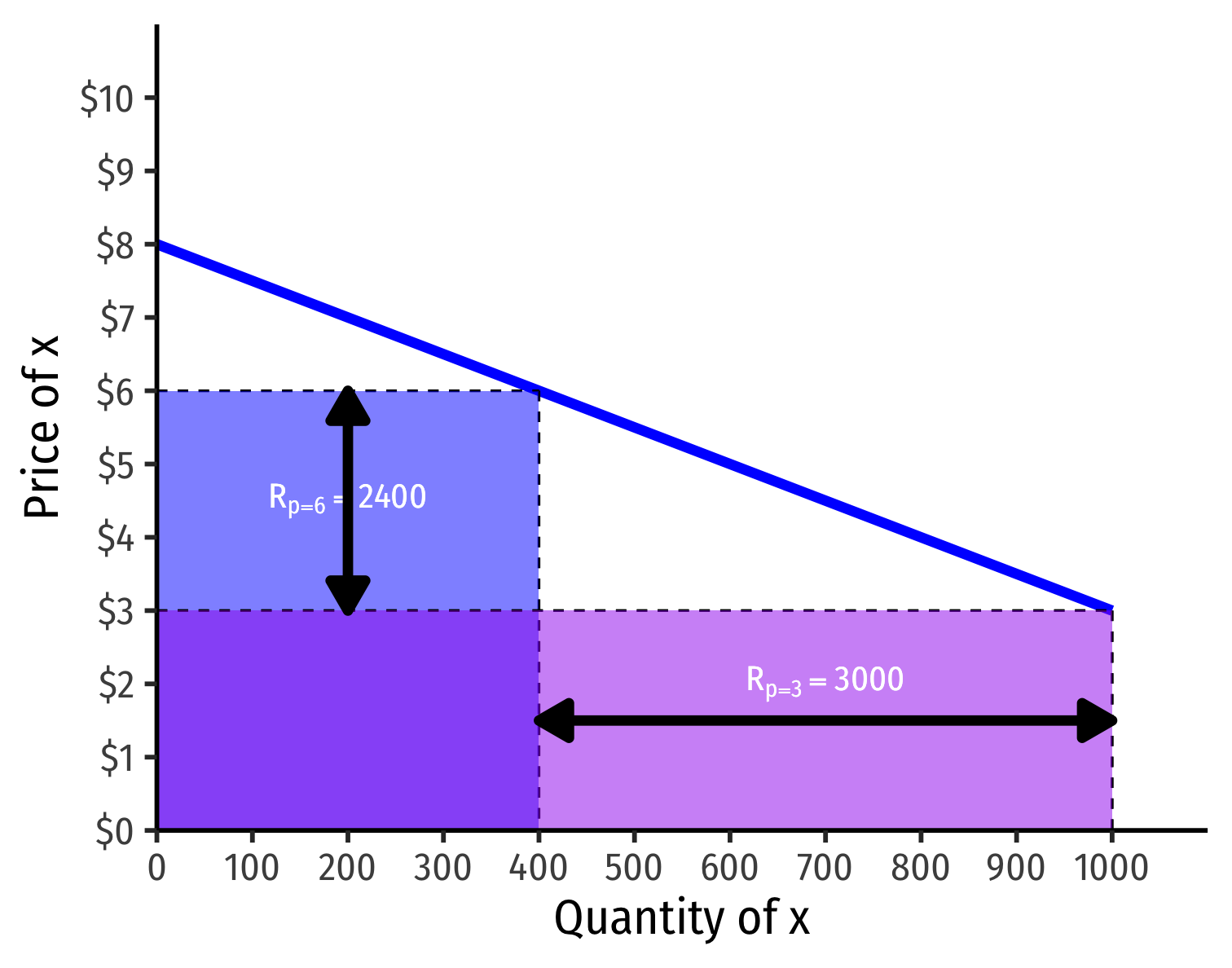
Price Elasticity and Revenues
R(q)=pq
| q | p | R(q) |
|---|---|---|
| 0 | 10 | 0 |
| 1 | 9 | 9 |
| 2 | 8 | 16 |
| 3 | 7 | 21 |
| 4 | 6 | 24 |
| 5 | 5 | 25 |
| 6 | 4 | 24 |
| 7 | 3 | 21 |
| 8 | 2 | 16 |
| 9 | 1 | 9 |
| 10 | 0 | 0 |
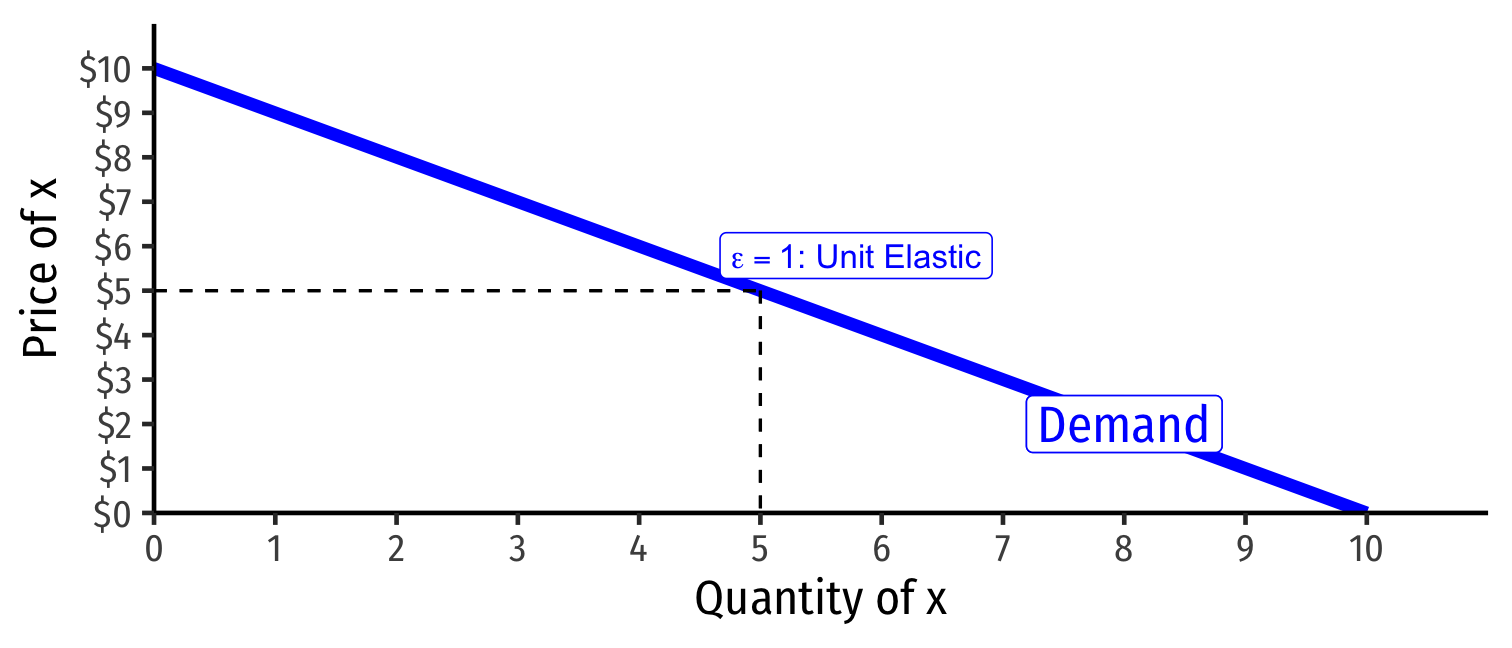
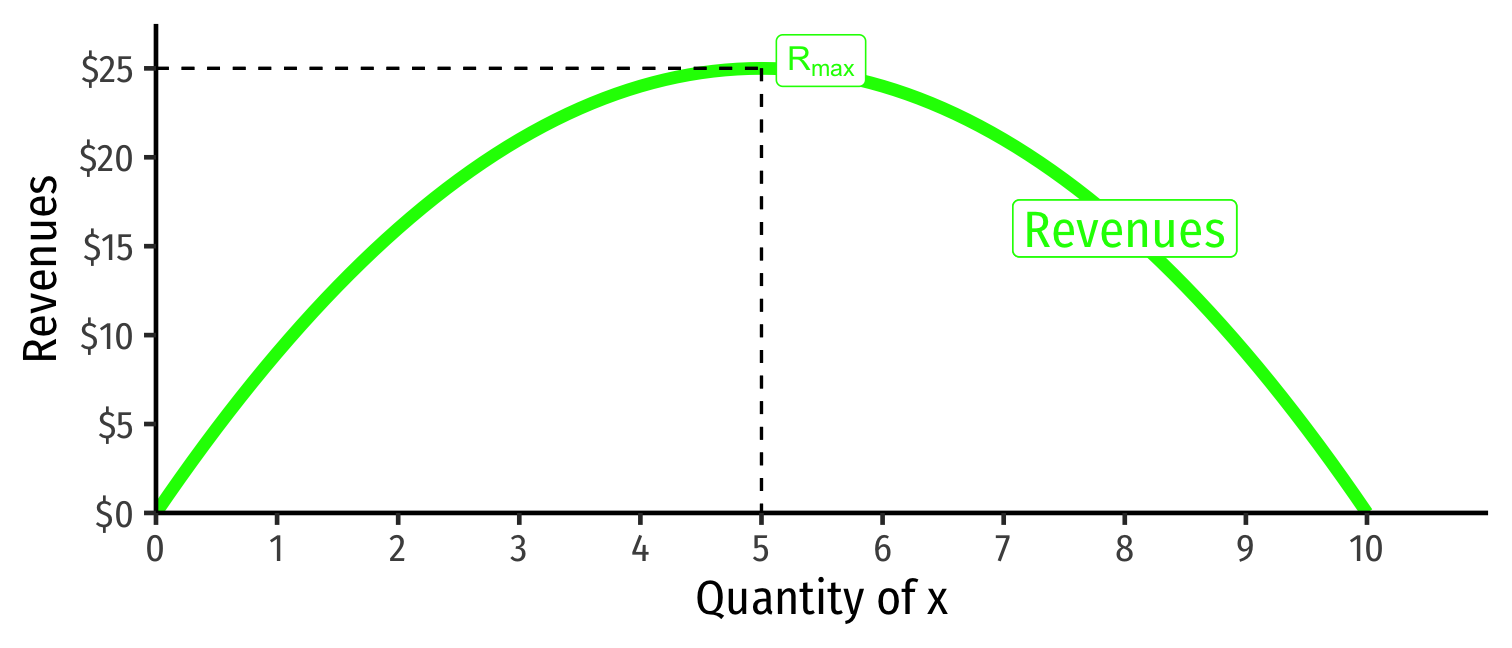
Revenue max'ed at price where ε=−1
Price Elasticity and Revenues: Example I

Source: CNN (July 2, 2018)
"Build-A-Bear announced its Pay Your Age event earlier this week. Customers who show up to the stores can pay their current age for the popular stuffed animals. On Wednesday, the retailer wrote on its Facebook page that it was 'anticipating potential of long lines and wait times.'"
Price Elasticity and Revenues: Example II
"While leaguewide average attendance dropped .43% this season to its lowest level since 2010, Atlanta’s attendance rose for the second season. Mercedes-Benz Stadium and the Falcons have become the model for drawing fans and keeping them happy."
"Instead of charging elevated sums—a long-held industry practice that fans despised—the Falcons would price most of its food at what it sold for on the street...Prices plunged 50%. Fans rejoiced. Although the team made less money on each $2 hot dog it sold, it made more overall. Average fan spending per game rose 16%. Atlanta’s food services, which ranked 18th in the NFL in the 2016 annual league survey, shot up to No. 1 in 2017 in every metric—and by a wide margin."
Price Elasticity and Revenues: Example III

Cowen & Tabarrok (2014: p.75)
Price Elasticity and Revenues: Example IV
Summing Up Unit 1
Models of Individual Choice I

"All models are lies. The art is telling useful lies." - George Box
Remember, we're not modelling the process by which people actually choose
We're predicting consequences (in people's choices) when parameters change
Models of Individual Choice II
Constrained optimization models are the main workhorse model in economics
All constrained optimization models have three moving parts:
Choose: < some alternative >
In order to maximize: < some objective >
Subject to: < some constraints >

Models of Individual Choice III

Applications of Consumer Theory
- See today's class notes page for some applications of consumer theory:
Uncertainty: risky outcomes & insurance
Exchange: two individuals trading their endowments, general equilibrium, & Pareto efficiency
Taxes: Which is better for consumers, a consumption tax or a (revenue-equivalent) income tax?
Intertemporal choice: saving, borrowing, lending, & interest
