2.6 — Long Run Industry Equilibrium
ECON 306 • Microeconomic Analysis • Spring 2023
Ryan Safner
Associate Professor of Economics
safner@hood.edu
ryansafner/microS23
microS23.classes.ryansafner.com
Firm's Long Run Supply Decisions
Firm Decisions in the Long Run I
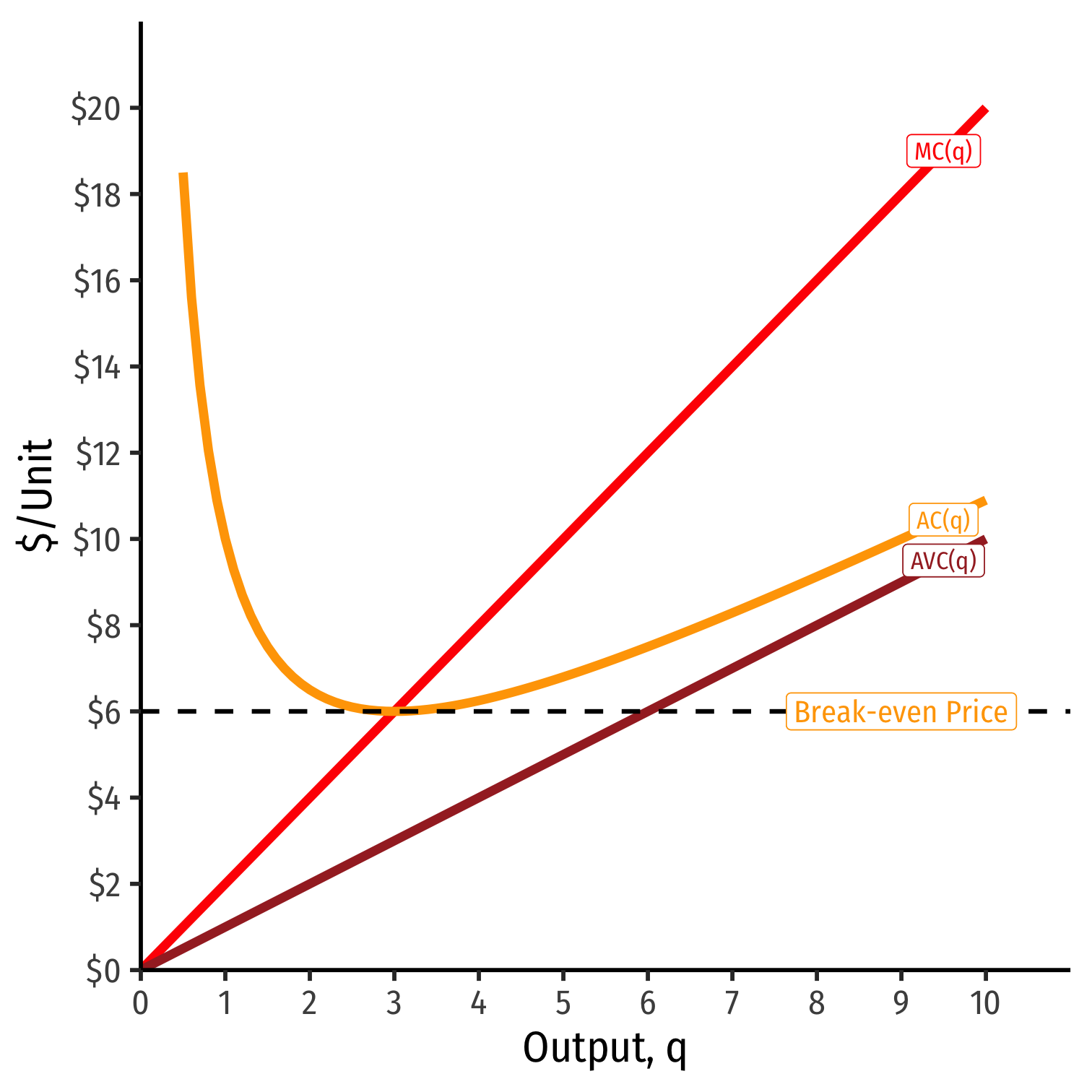
Minimum AC(q): market price of $6.00
- Firms break even and earn “normal” economic profits (of $0)
At any market price below $6.00, firm earns losses
- Short Run: firm shuts down only if p<AVC(q)p<AVC(q)
At any market price above $6.00, firm earns “supernormal” profits (>$0)
Firm Supply Decisions in the Short Run vs. Long Run
- Short run: firms that shut down (q∗=0)(q∗=0) are stuck in market, incur fixed costs π=−fπ=−f
Firm Supply Decisions in the Short Run vs. Long Run
Short run: firms that shut down (q∗=0)(q∗=0) are stuck in market, incur fixed costs π=−fπ=−f
Long run: firms earning losses (π<0)(π<0) can exit the market and earn π=0π=0
- No more fixed costs, firms can sell/abandon ff

Firm Supply Decisions in the Short Run vs. Long Run
Short run: firms that shut down (q∗=0)(q∗=0) are stuck in market, incur fixed costs π=−fπ=−f
Long run: firms earning losses (π<0)(π<0) can exit the market and earn π=0π=0
- No more fixed costs, firms can sell/abandon ff
Entrepreneurs not currently in market can enter and produce, if entry would earn them π>0π>0


Firm Supply Decisions in the Short Run vs. Long Run

Firm Supply Decisions in the Short Run vs. Long Run


Firm's Long Run Supply: Visualizing
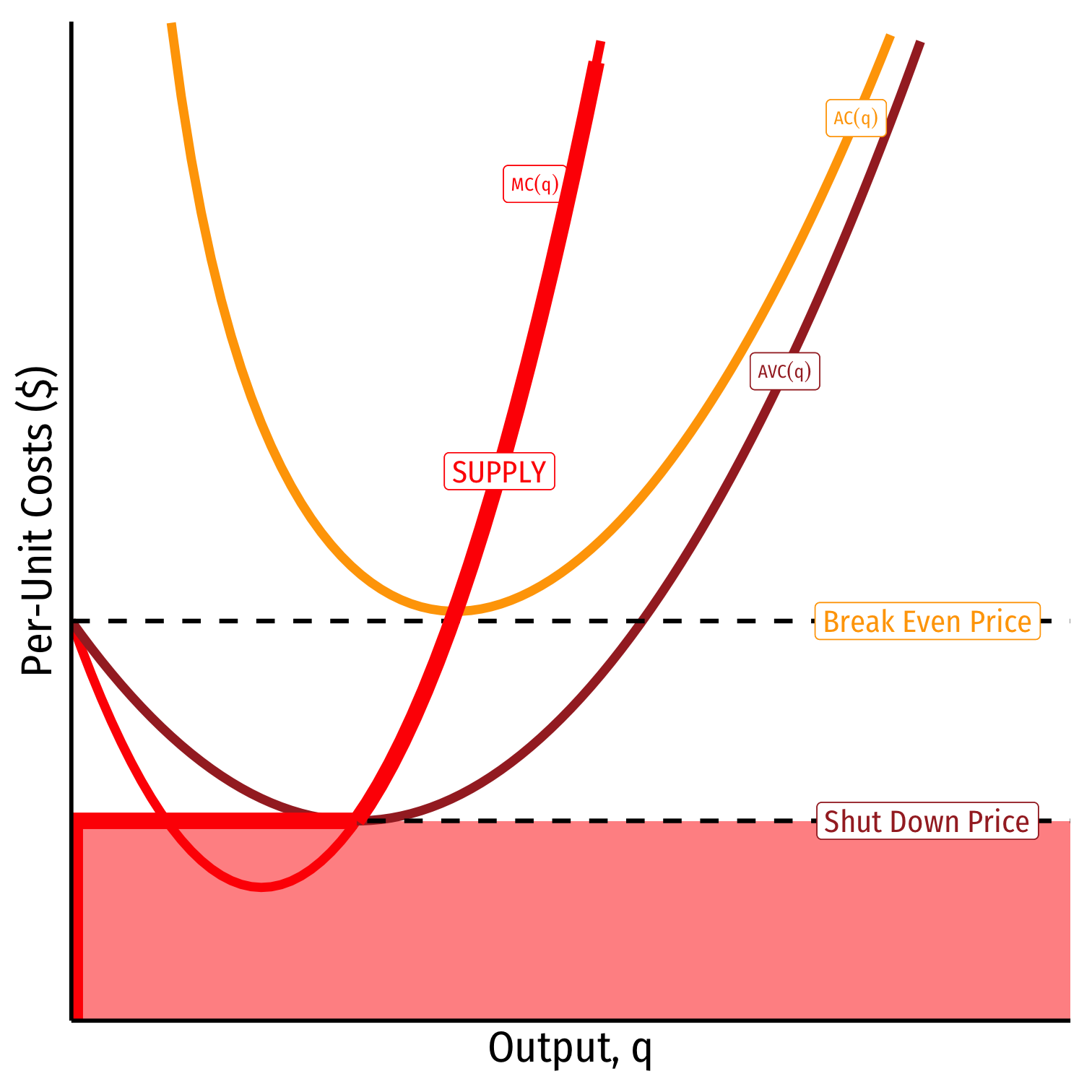
When p<AVCp<AVC
Profits are negative
Short run: shut down production
- Firm loses more ππ by producing than by not producing
Long run: firms in industry exit the industry
- No new firms will enter this industry
Firm's Long Run Supply: Visualizing
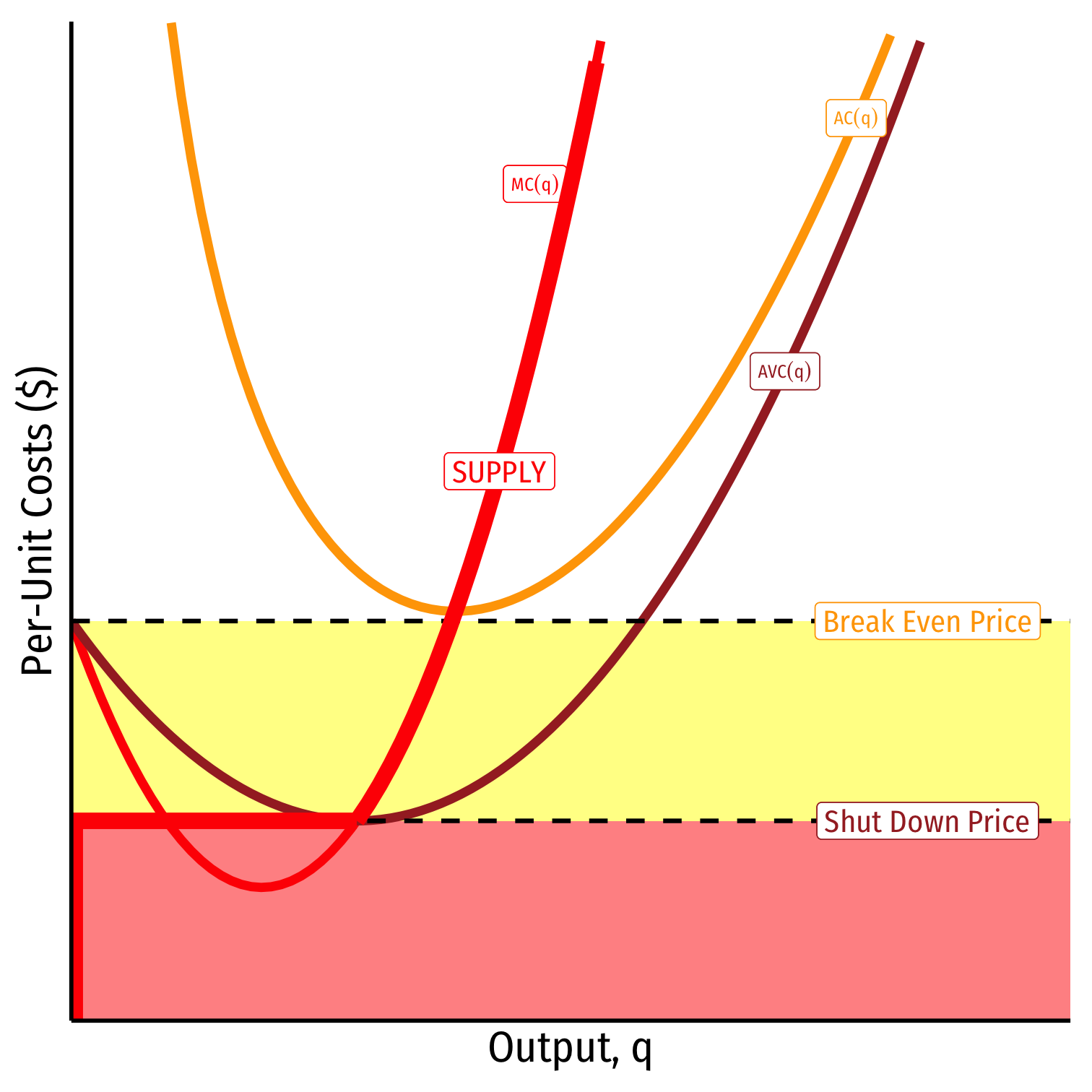
When AVC<p<ACAVC<p<AC
Profits are negative
Short run: continue production
- Firm loses less ππ by producing than by not producing
Long run: firms in industry exit the industry
- No new firms will enter this industry
Firm's Long Run Supply: Visualizing
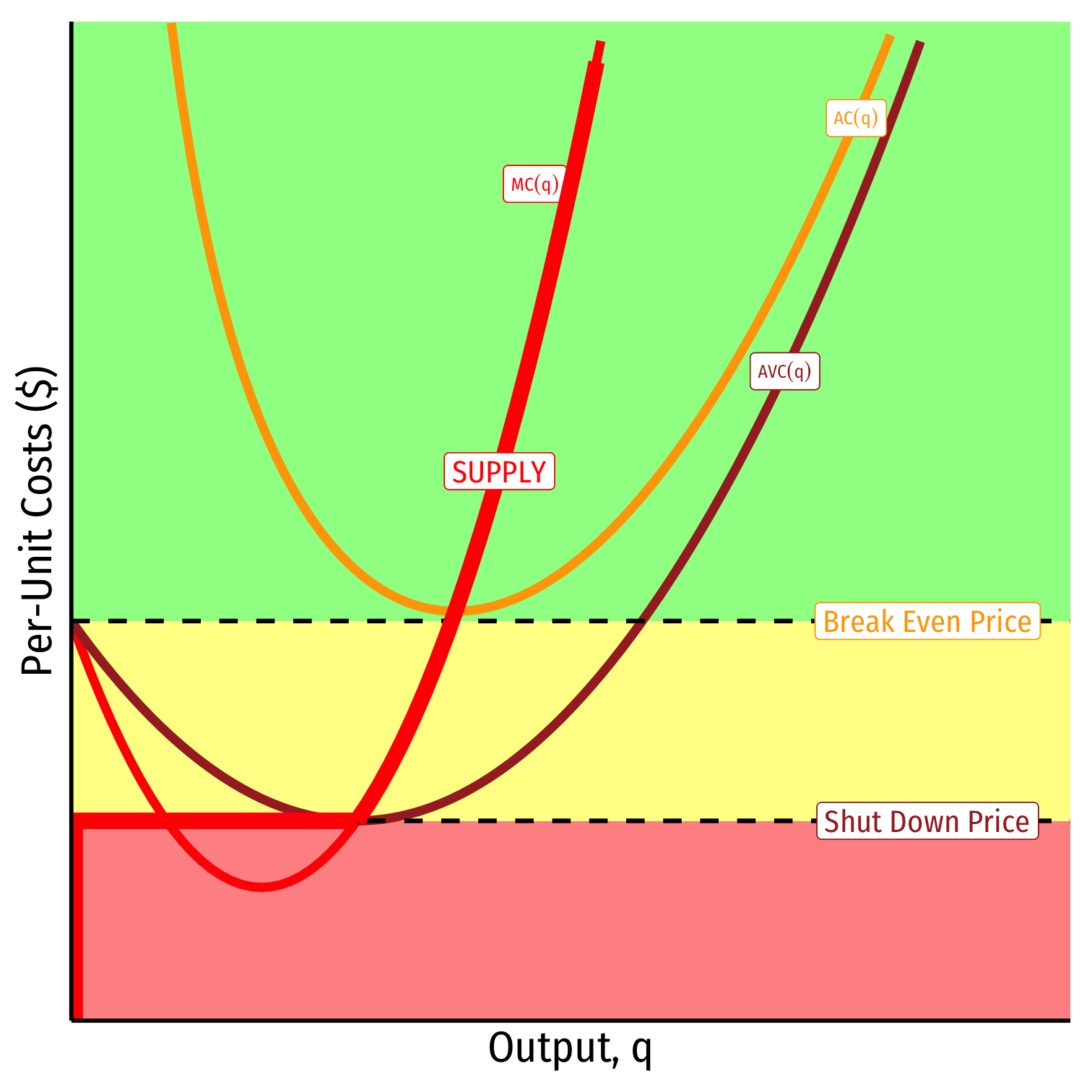
When AC<pAC<p
Profits are positive
Short run: continue production
- Firm earning profits
Long run: firms in industry stay in industry
- New firms will enter this industry
Production Rules, Updated:
1. Choose q∗q∗ such that MR(q)=MC(q)MR(q)=MC(q)
2. Profit π=q[p−AC(q)]π=q[p−AC(q)]
3. Shut down in short run if p<AVC(q)p<AVC(q)
4. Exit in long run if p<AC(q)p<AC(q)

Market Entry and Exit
Exit, Entry, and Long Run Industry Equilibrium I
Now we must combine optimizing individual firms with market-wide adjustment to equilibrium
Since π=[p−AC(q)]qπ=[p−AC(q)]q, in the long run, profit-seeking firms will:
Exit, Entry, and Long Run Industry Equilibrium I
Now we must combine optimizing individual firms with market-wide adjustment to equilibrium
Since π=[p−AC(q)]qπ=[p−AC(q)]q, in the long run, profit-seeking firms will:
- Enter markets where p>AC(q)p>AC(q)

Exit, Entry, and Long Run Industry Equilibrium I
Now we must combine optimizing individual firms with market-wide adjustment to equilibrium
Since π=[p−AC(q)]qπ=[p−AC(q)]q, in the long run, profit-seeking firms will:
- Enter markets where p>AC(q)p>AC(q)
- Exit markets where p<AC(q)p<AC(q)


Exit, Entry, and Long Run Industry Equilibrium II
- Long-run equilibrium: entry and exit ceases when p=AC(q)p=AC(q) for all firms, implying normal economic profits of π=0π=0

Exit, Entry, and Long Run Industry Equilibrium II
Long-run equilibrium: entry and exit ceases when p=AC(q)p=AC(q) for all firms, implying normal economic profits of π=0π=0
More generally, no marginal firm can profitably enter the industry
Long run economic profits for all firms in a competitive industry are 0
Firms must earn an accounting profit to stay in business

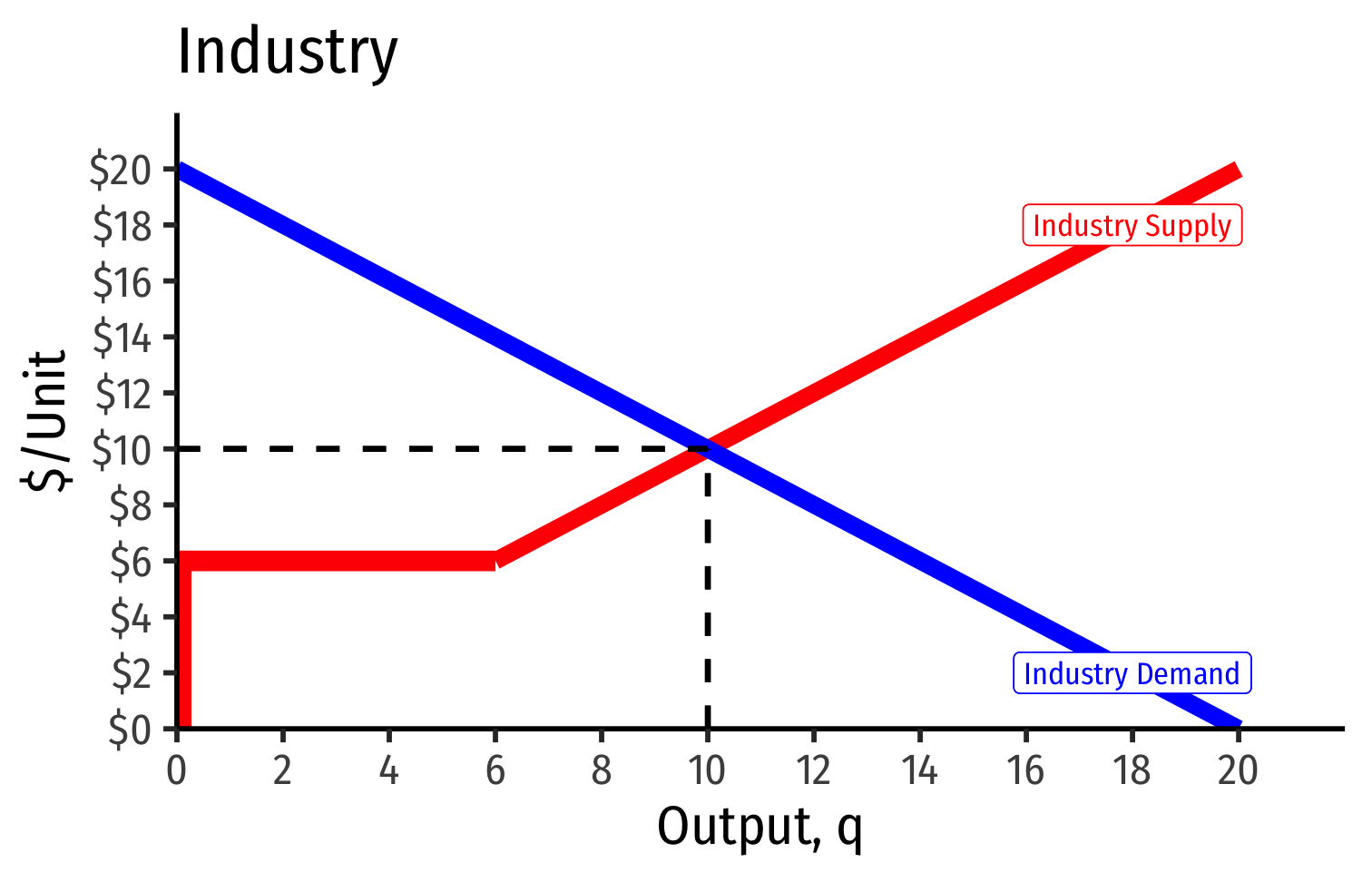
Deriving the Industry Supply Curve
The Industry Supply Curve
Industry supply curve: horizontal sum of all individual firms' supply curves
- recall: (MC(q)(MC(q) curve above AVCmin)AVCmin) (shut down price)
To keep it simple on the following slides:
- assume no fixed costs, so AC(q)=AVC(q)AC(q)=AVC(q)
- then industry supply curve is sum of individual MC(q)MC(q) curves above AC(q)minAC(q)min
Industry Supply Curves (Identical Firms)
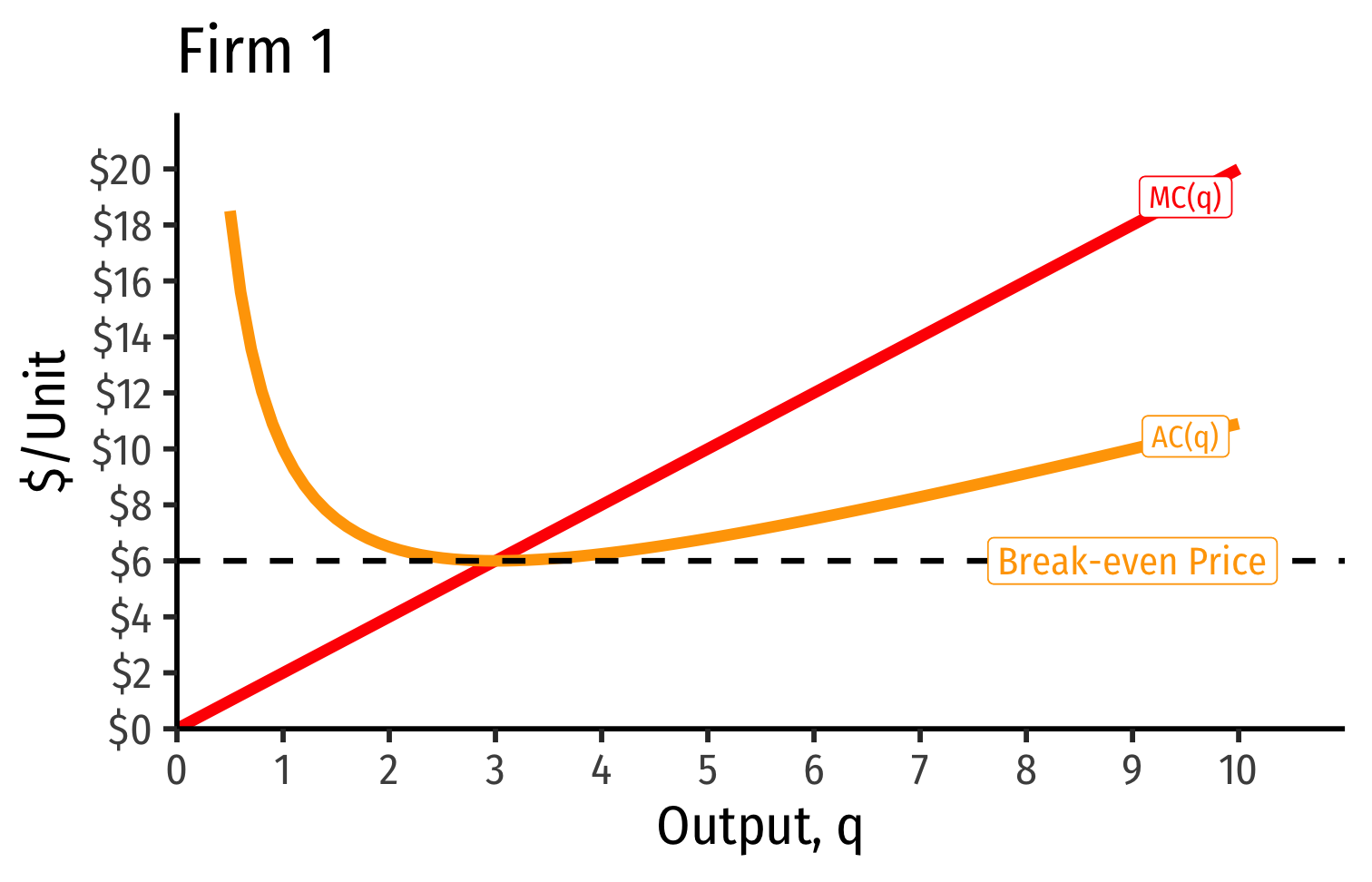
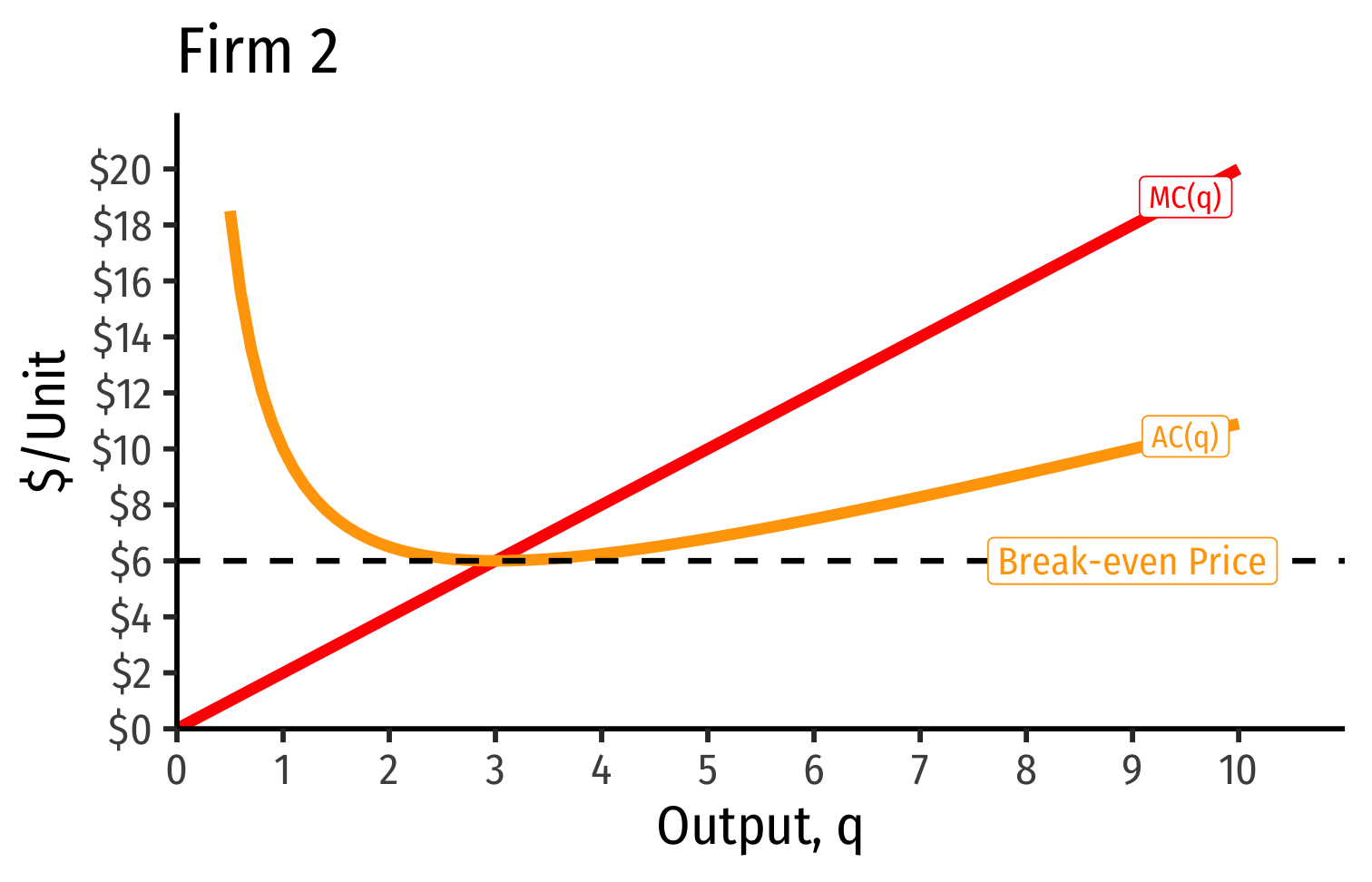
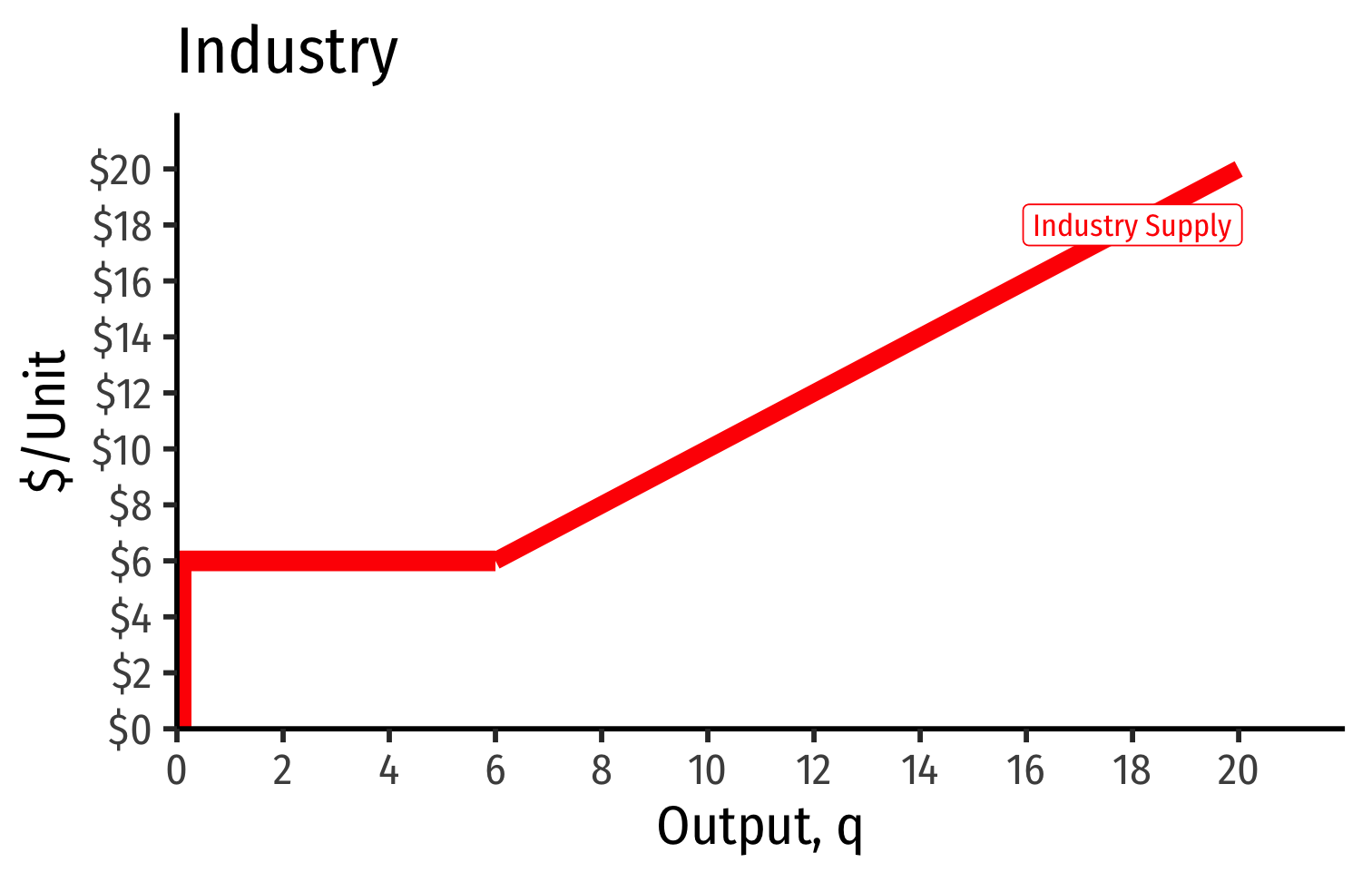
Industry Supply Curves (Identical Firms)



- Industry supply curve is the horizontal sum of all individual firm's supply curves
- Which are each firm's marginal cost curve above its breakeven price
Industry Supply Curves (Identical Firms)
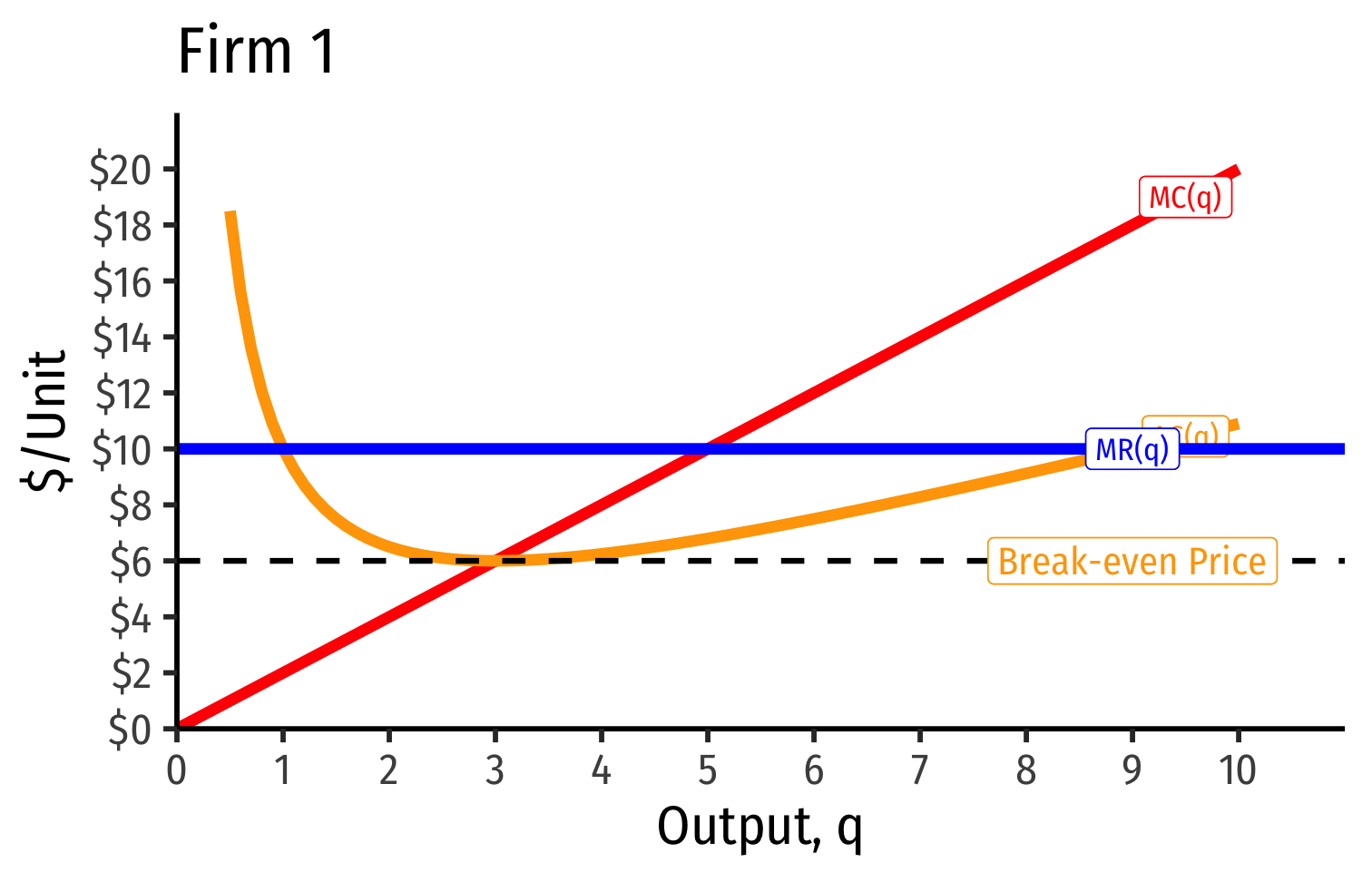
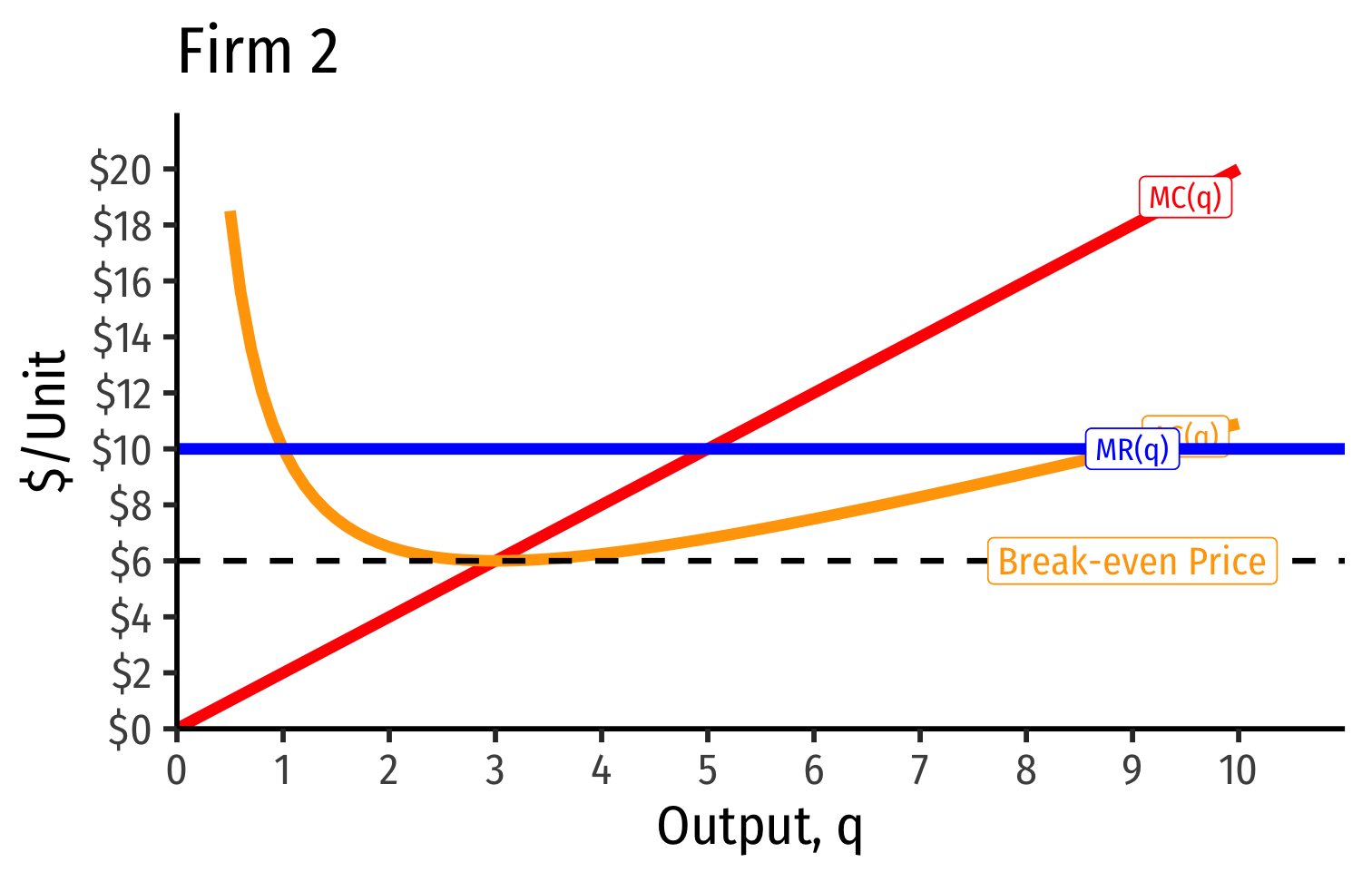
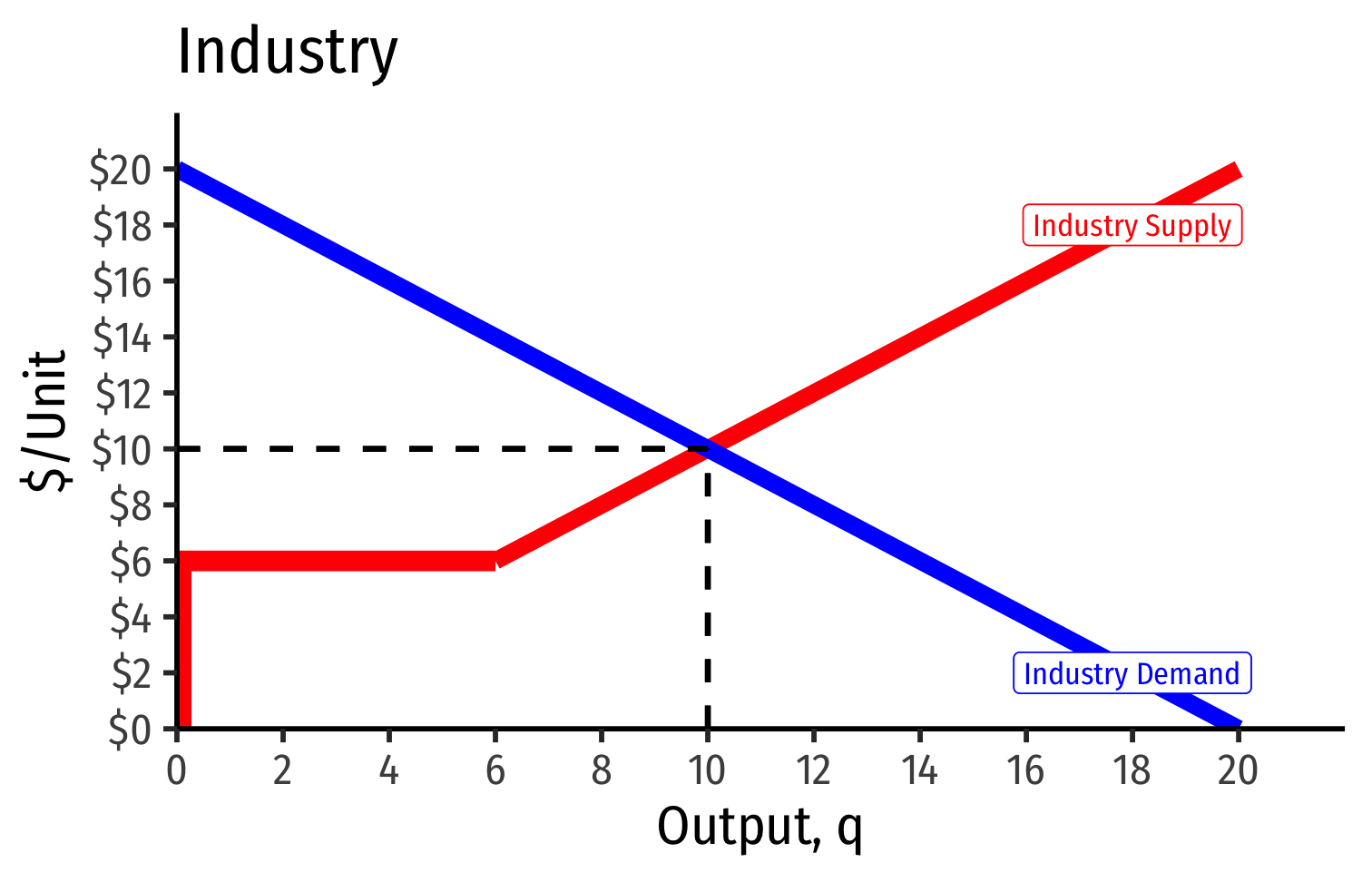
- Industry demand curve (where equal to supply) sets market price, demand for firms
Industry Supply Curves (Identical Firms)
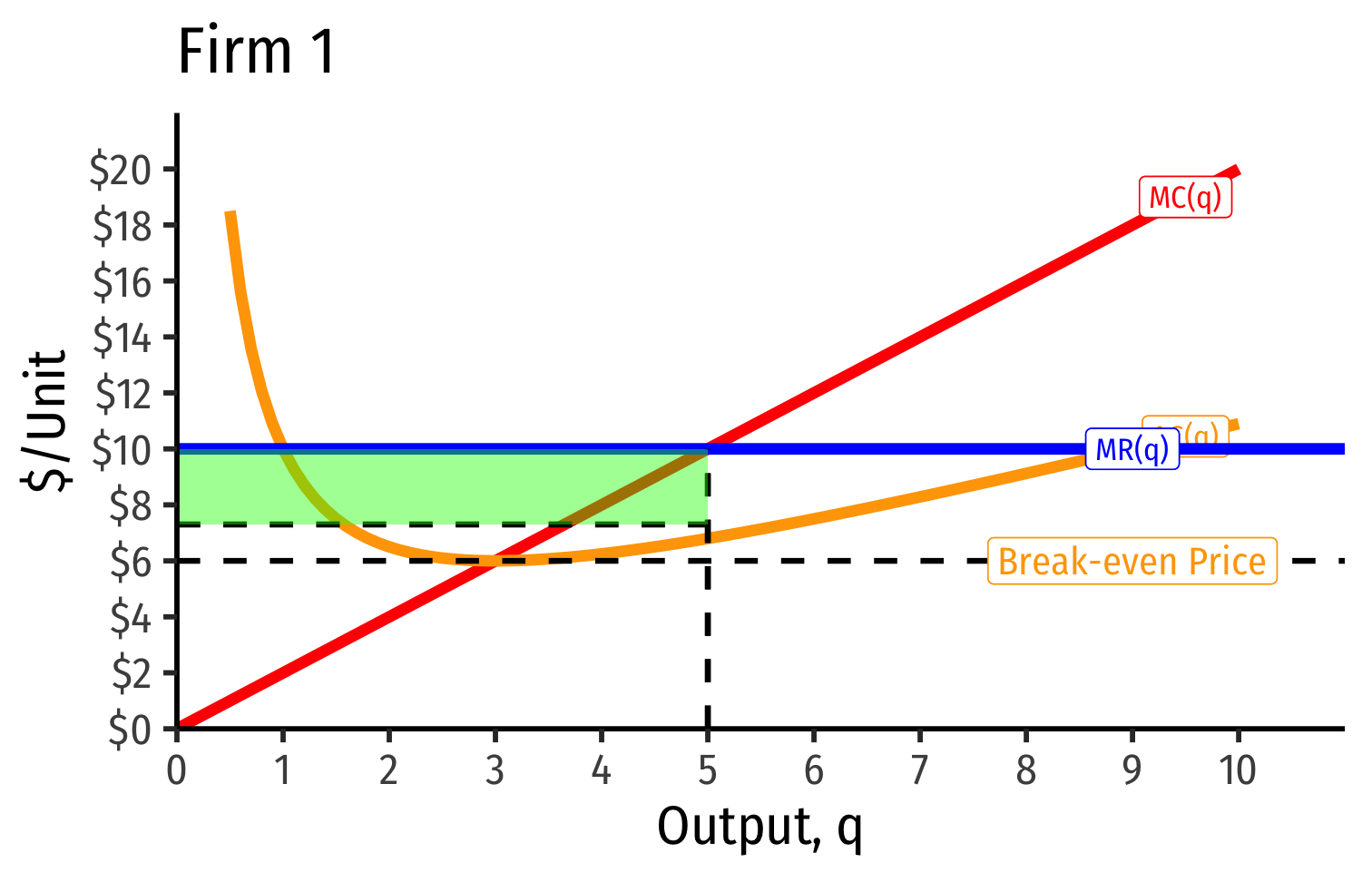
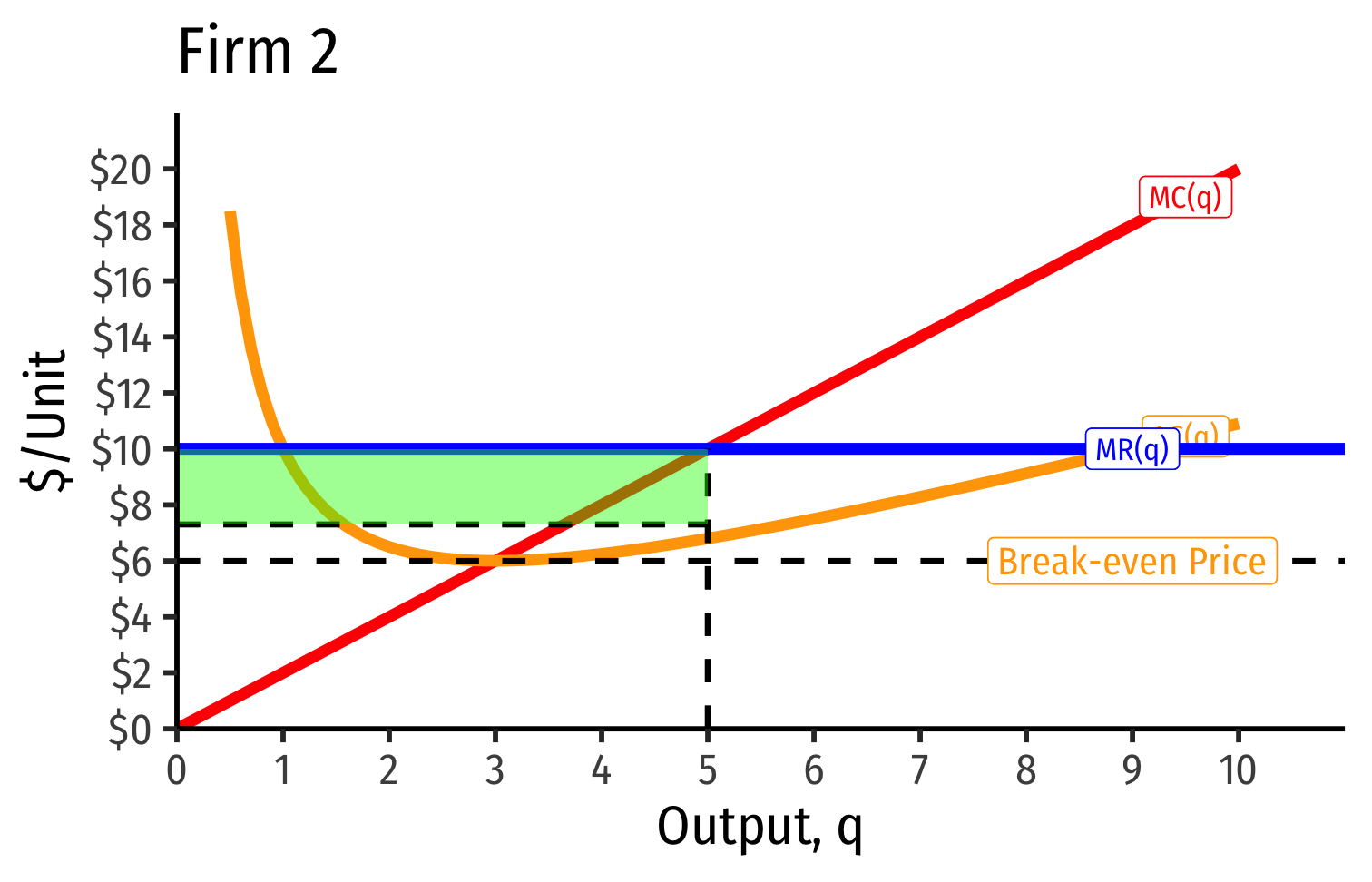
- Short Run: each firm is earning profits p>AC(q)p>AC(q)
Industry Supply Curves (Identical Firms)
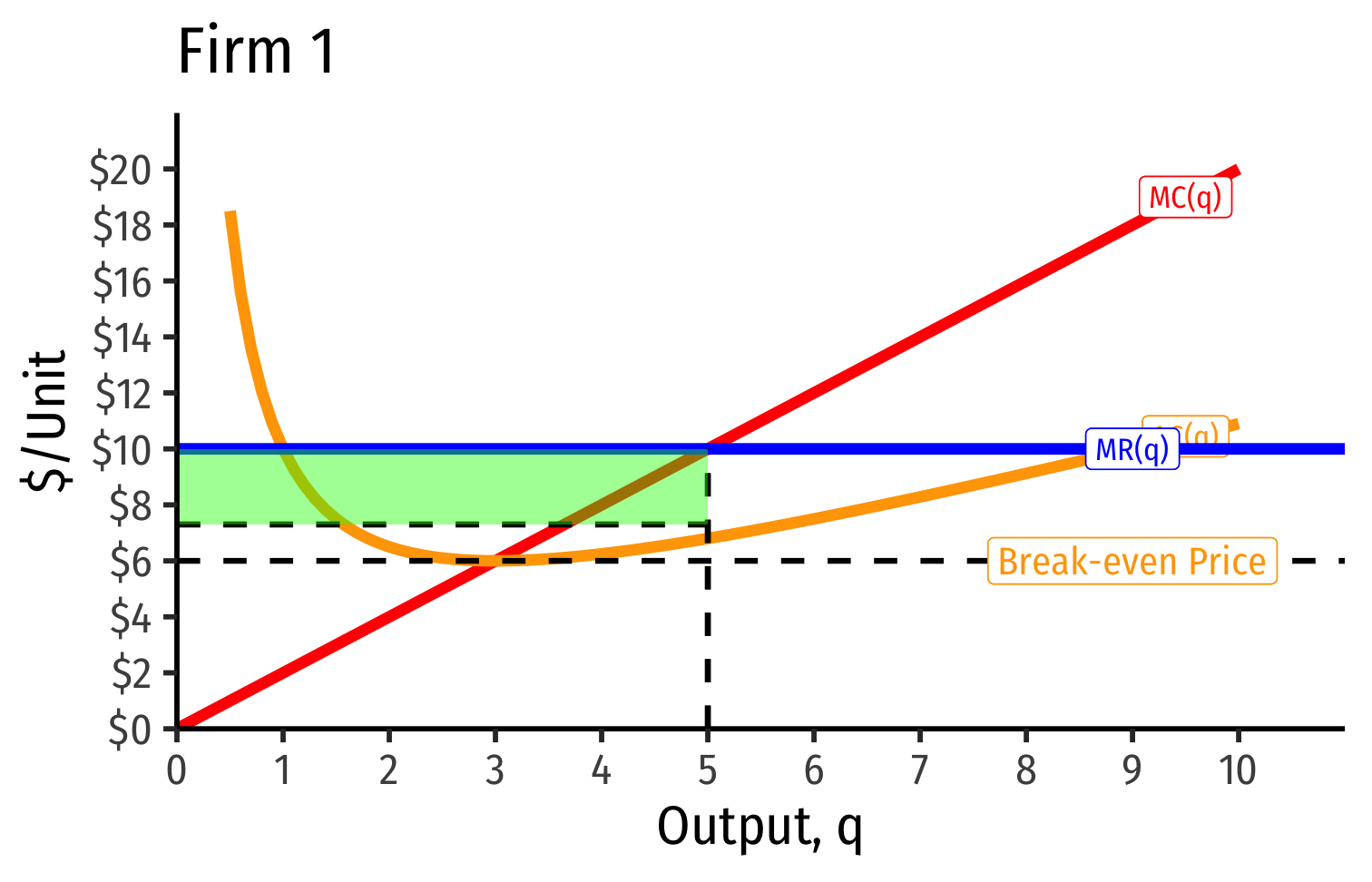
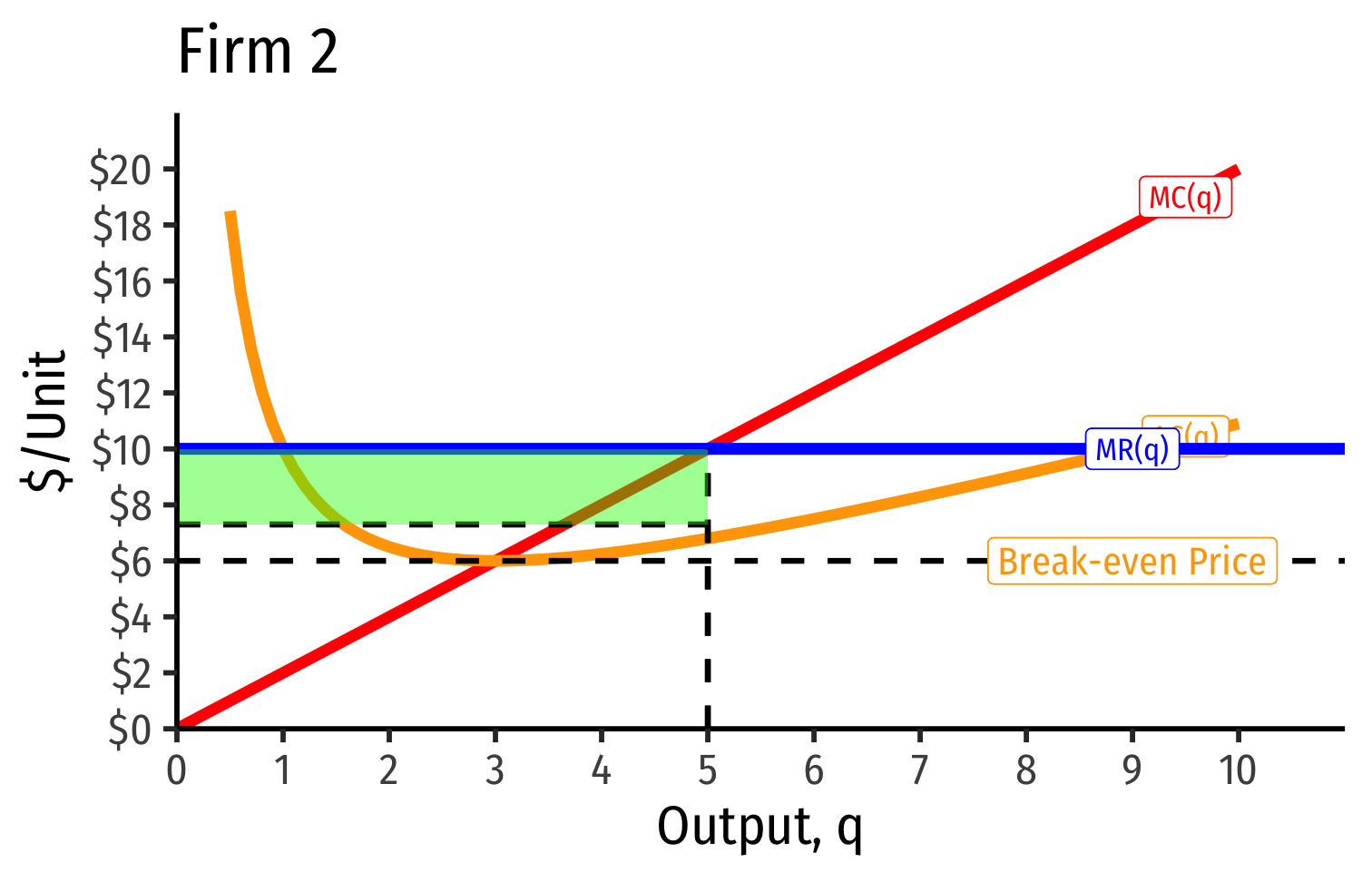
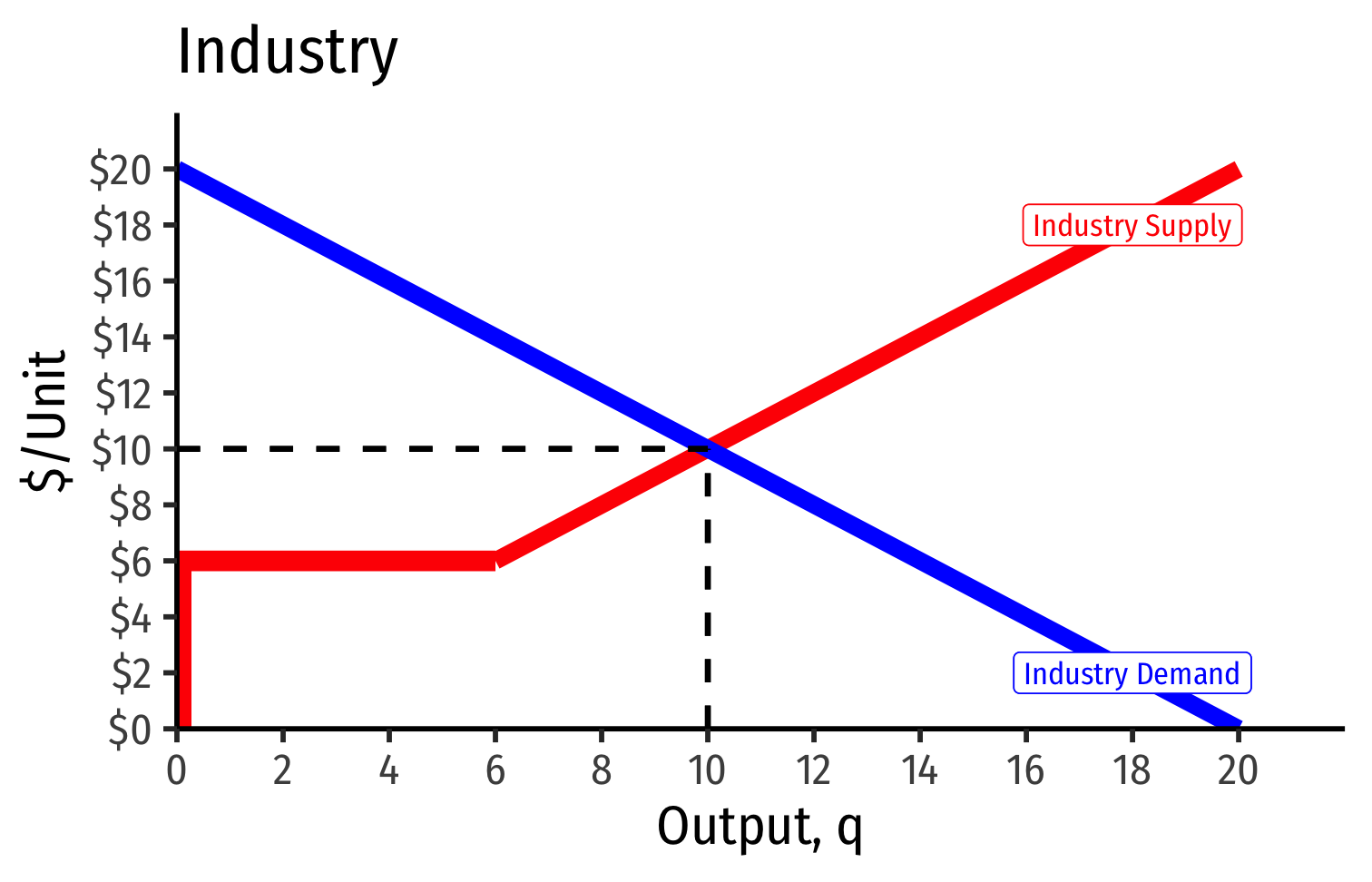
Short Run: each firm is earning profits p>AC(q)p>AC(q)
Long run: induces entry by firm 3, firm 4, ⋯⋯, firm nn
Industry Supply Curves (Identical Firms)



Short Run: each firm is earning profits p>AC(q)p>AC(q)
Long run: induces entry by firm 3, firm 4, ⋯⋯, firm nn
- Long run industry equilibrium:
Industry Supply Curves (Identical Firms)
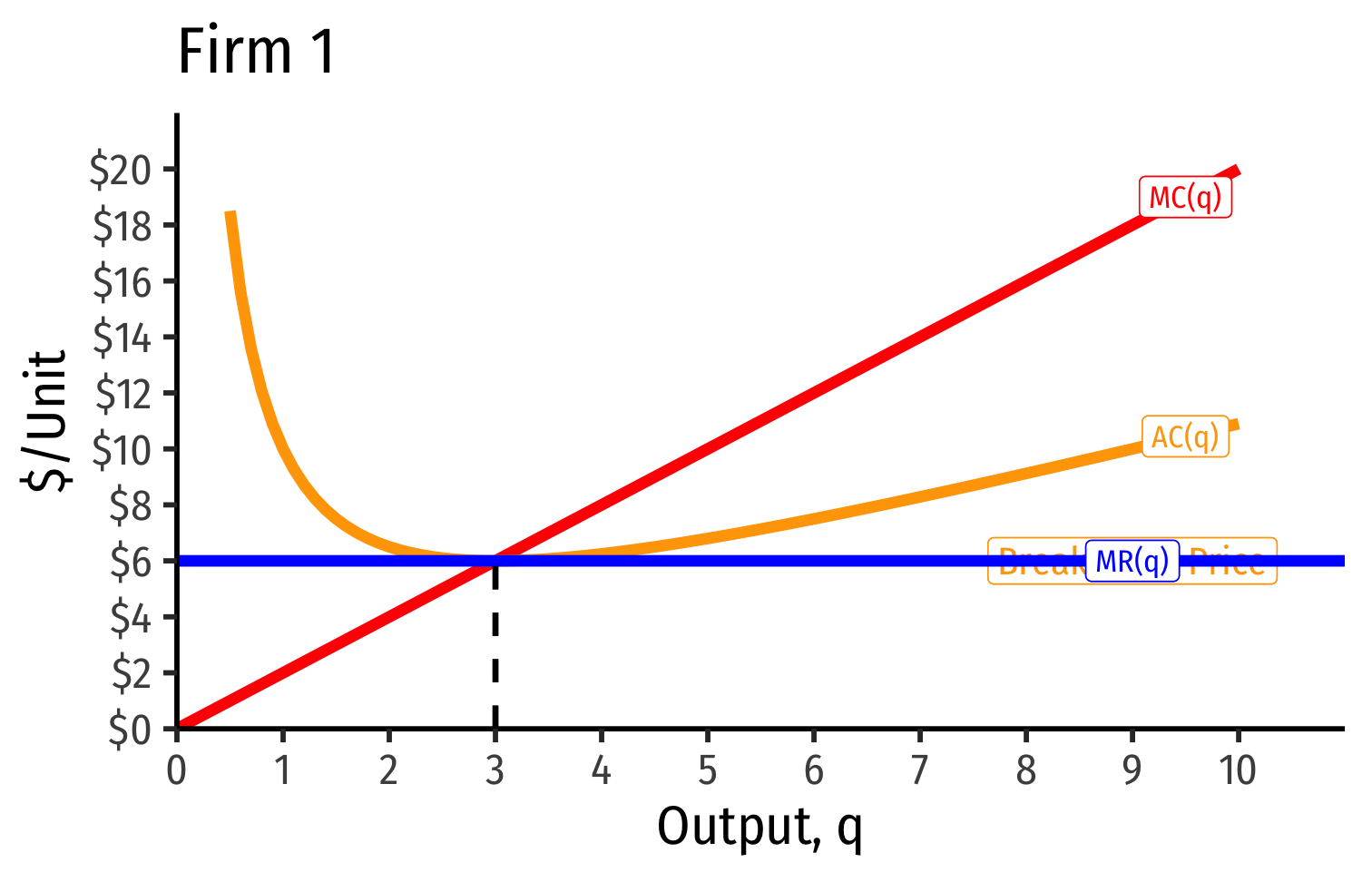
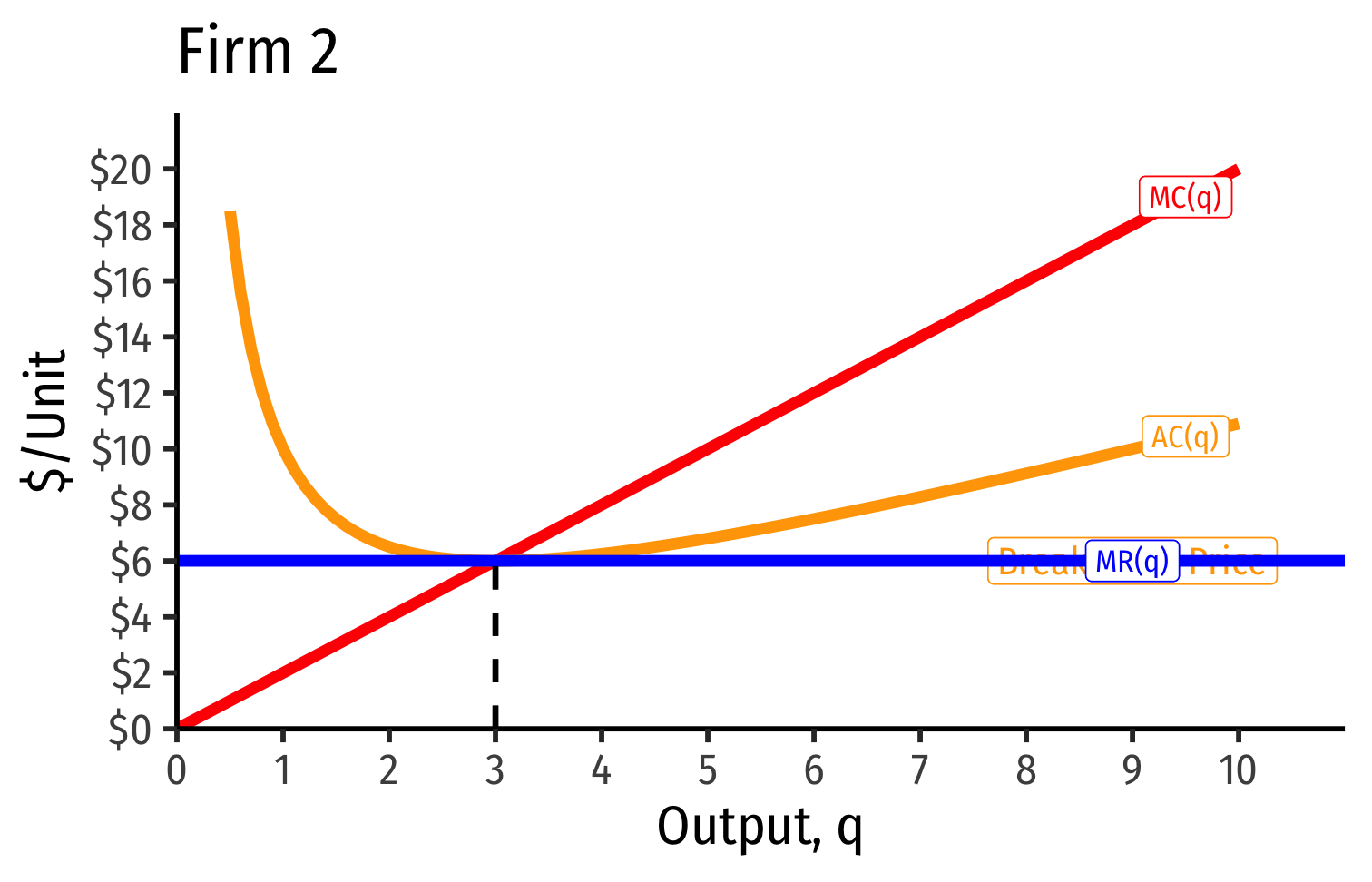
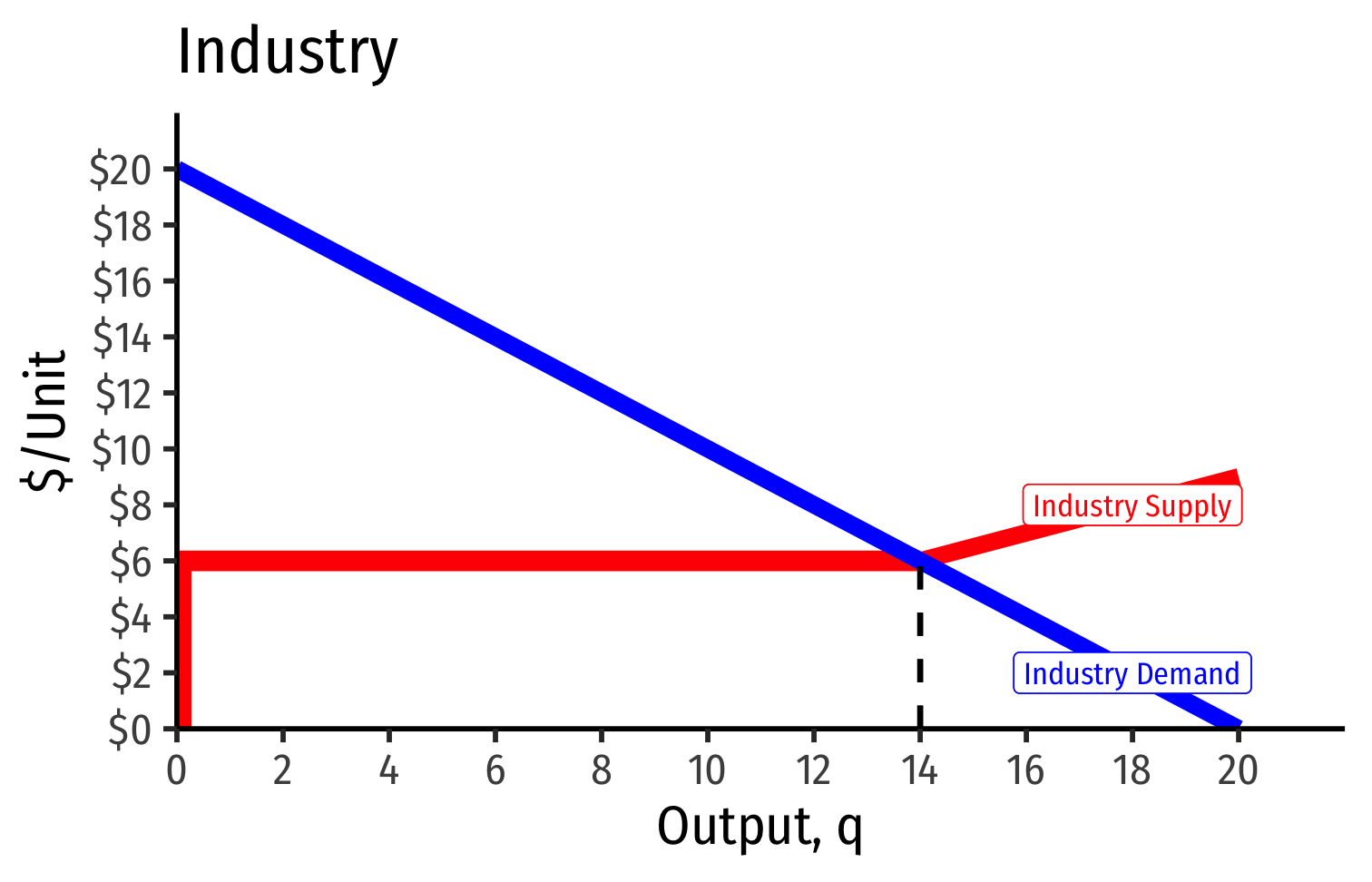
Short Run: each firm is earning profits p>AC(q)p>AC(q)
Long run: induces entry by firm 3, firm 4, ⋯⋯, firm nn
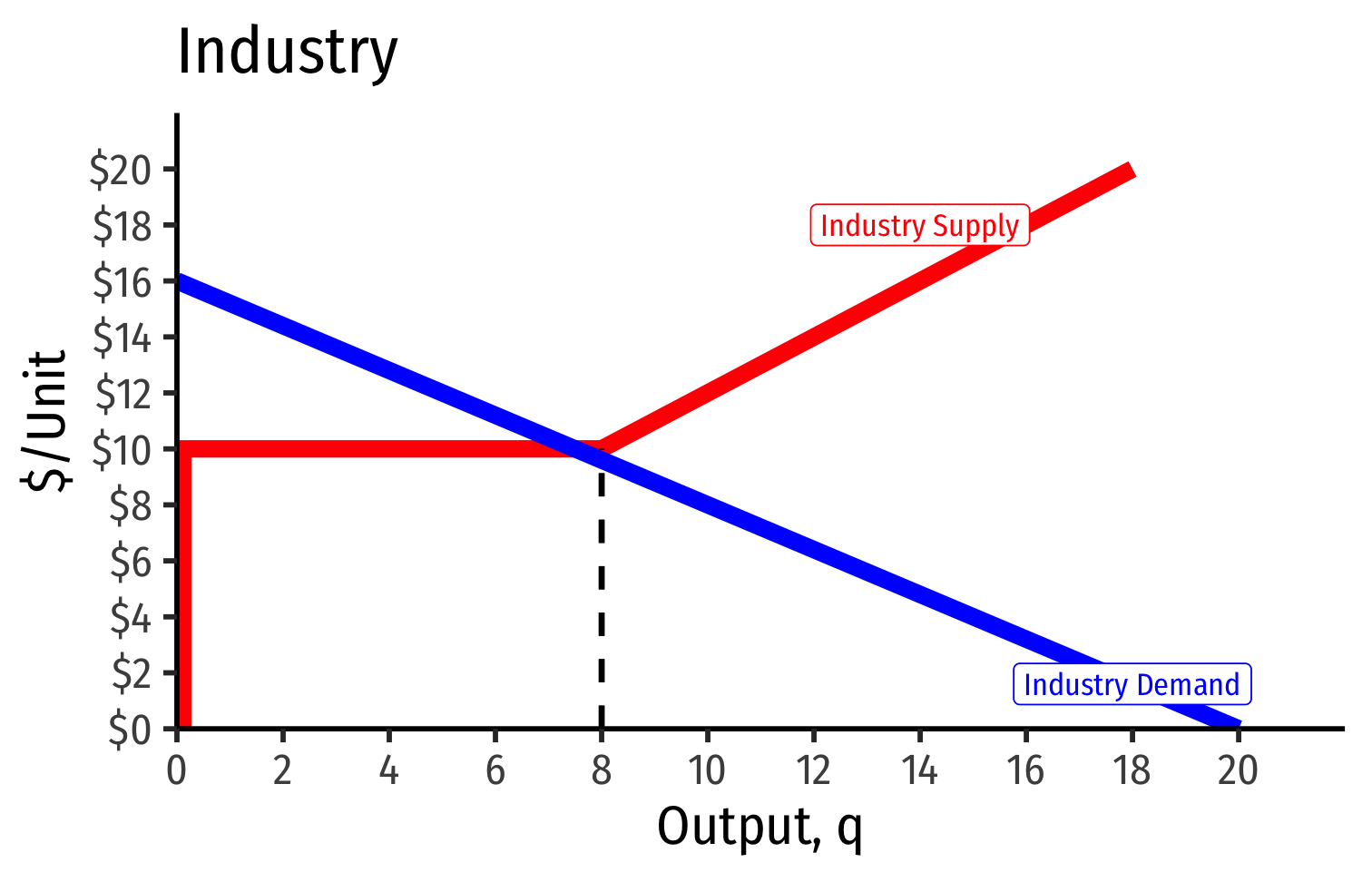
Long run industry equilibrium: p=AC(q)minp=AC(q)min, π=0π=0 at p=p= $6; supply becomes more elastic
Economic Rents, Profits, & Competition
Back to Zero Economic Profits
- Recall, we’ve essentially defined a firm as a mere replicable recipe (production function) of transforming resources
q=f(L,K)q=f(L,K)
- “Any idiot” can enter market, buy required (L,K)(L,K) at prices (w,r)(w,r), produce q∗q∗ at market price pp and earn the market rate of ππ
Back to Zero Economic Profits
Zero long run economic profit ≠≠ industry disappears, just stops growing
Less attractive to entrepreneurs & start ups to enter than other, more profitable industries
These are mature industries (again, often commodities), the backbone of the economy, just not sexy!

Back to Zero Economic Profits
p=MCp=MC
- All factors are paid their market price
- i.e. their opportunity cost — what they could earn elsewhere in economy
p=ACp=AC
- Firms earn normal market rate of return
- No excess rewards (economic profits) to attract new resources into the industry, nor losses to push resources out of industry
 p=MC=ACp=MC=AC
p=MC=ACp=MC=AC
Back to Zero Economic Profits
But we’ve so far been imagining a market where every firm is identical, just a recipe “any idiot” can copy
What about if firms have different technologies or costs?

Industry Supply Curves (Different Firms) I
Firms have different technologies/costs due to relative differences in:
- Managerial talent
- Worker talent
- Location
- First-mover advantage
- Technological secrets/IP
- License/permit access
- Political connections
- Lobbying
Let's derive industry supply curve again, and see how this may affect profits

Industry Supply Curves (Different Firms) II
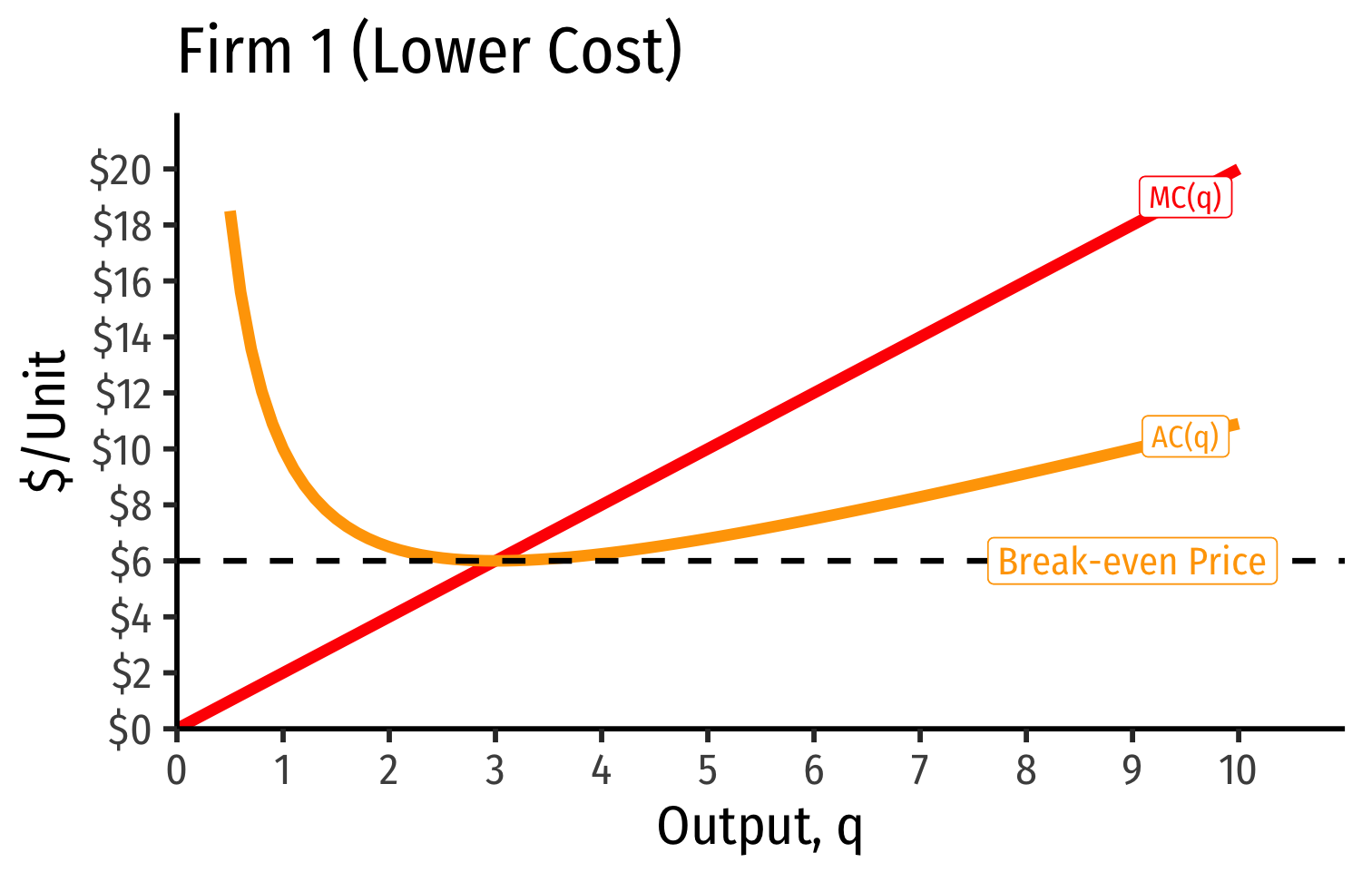
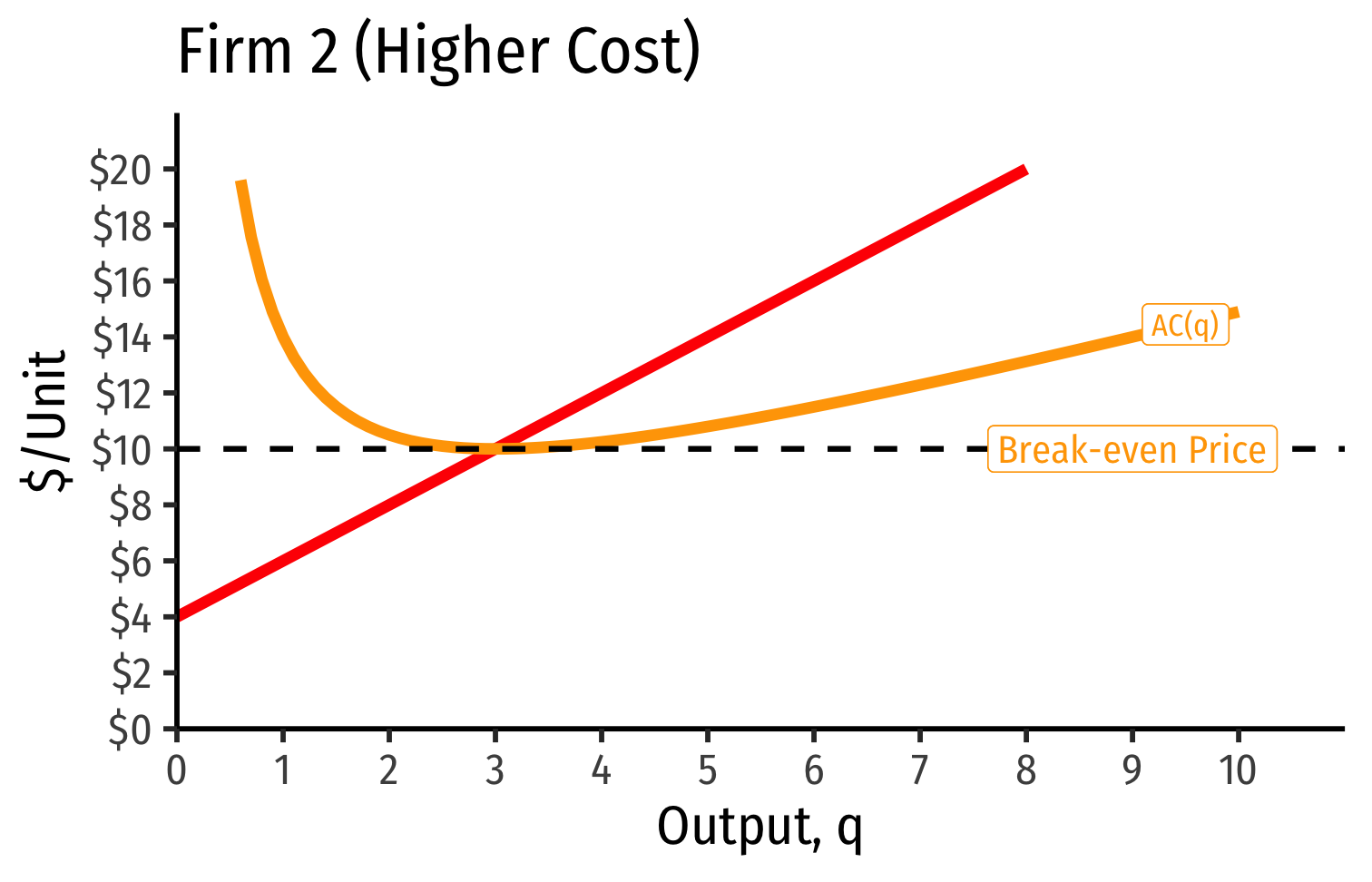
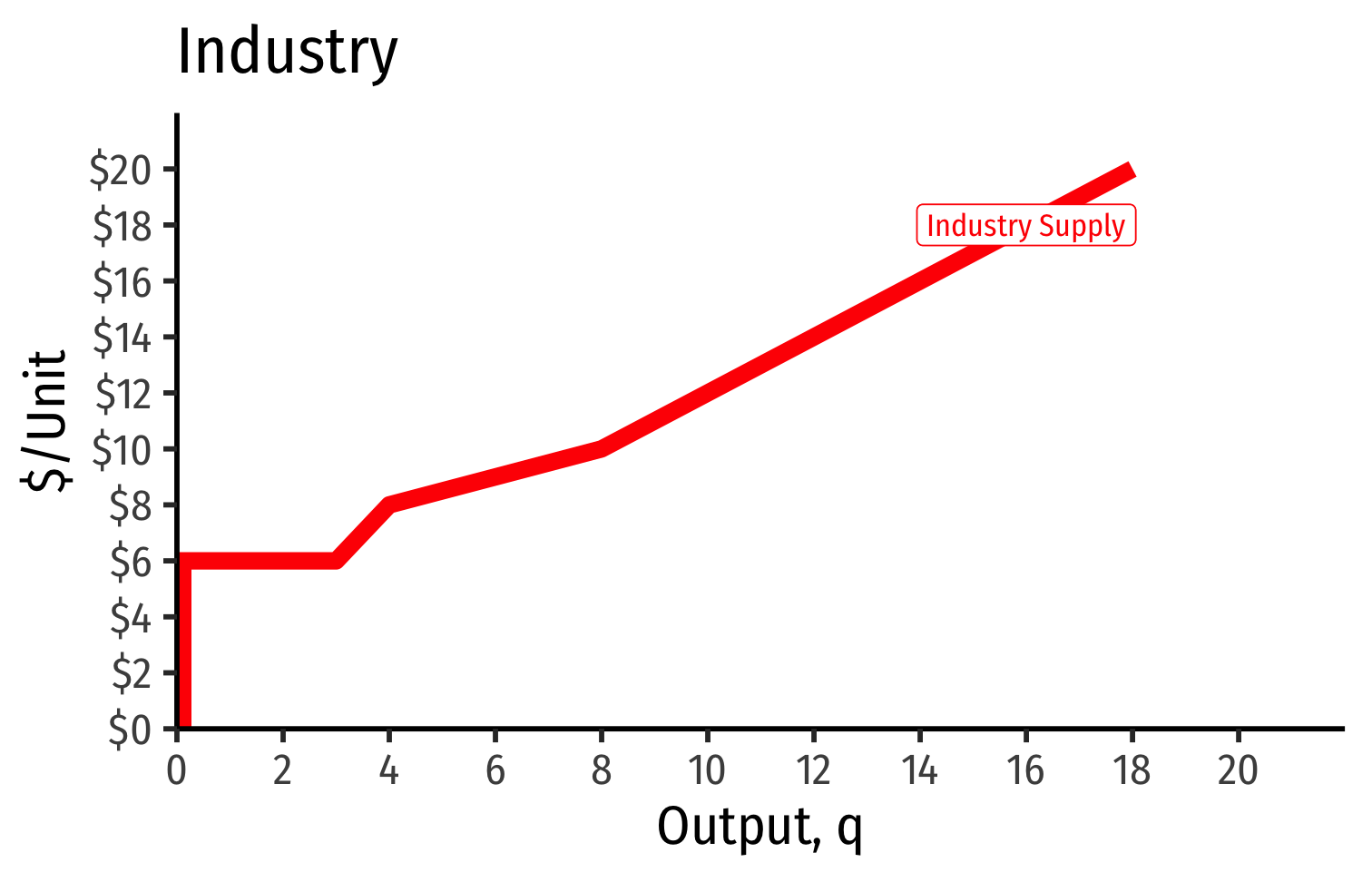
Industry Supply Curves (Different Firms) II



- Industry supply curve is the horizontal sum of all individual firm's supply curves
- Which are each firm's marginal cost curve above its breakeven price
Industry Supply Curves (Different Firms) II
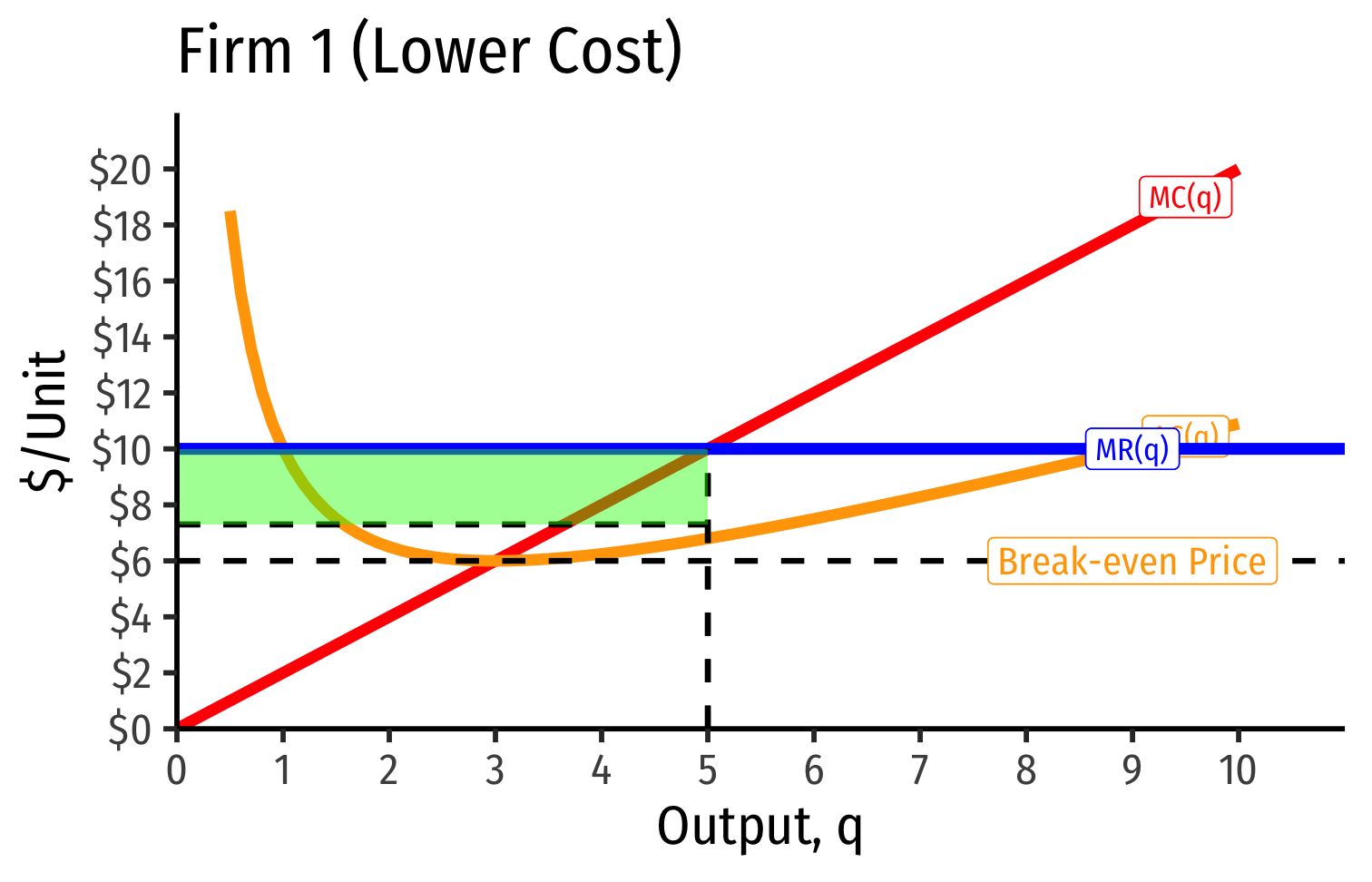
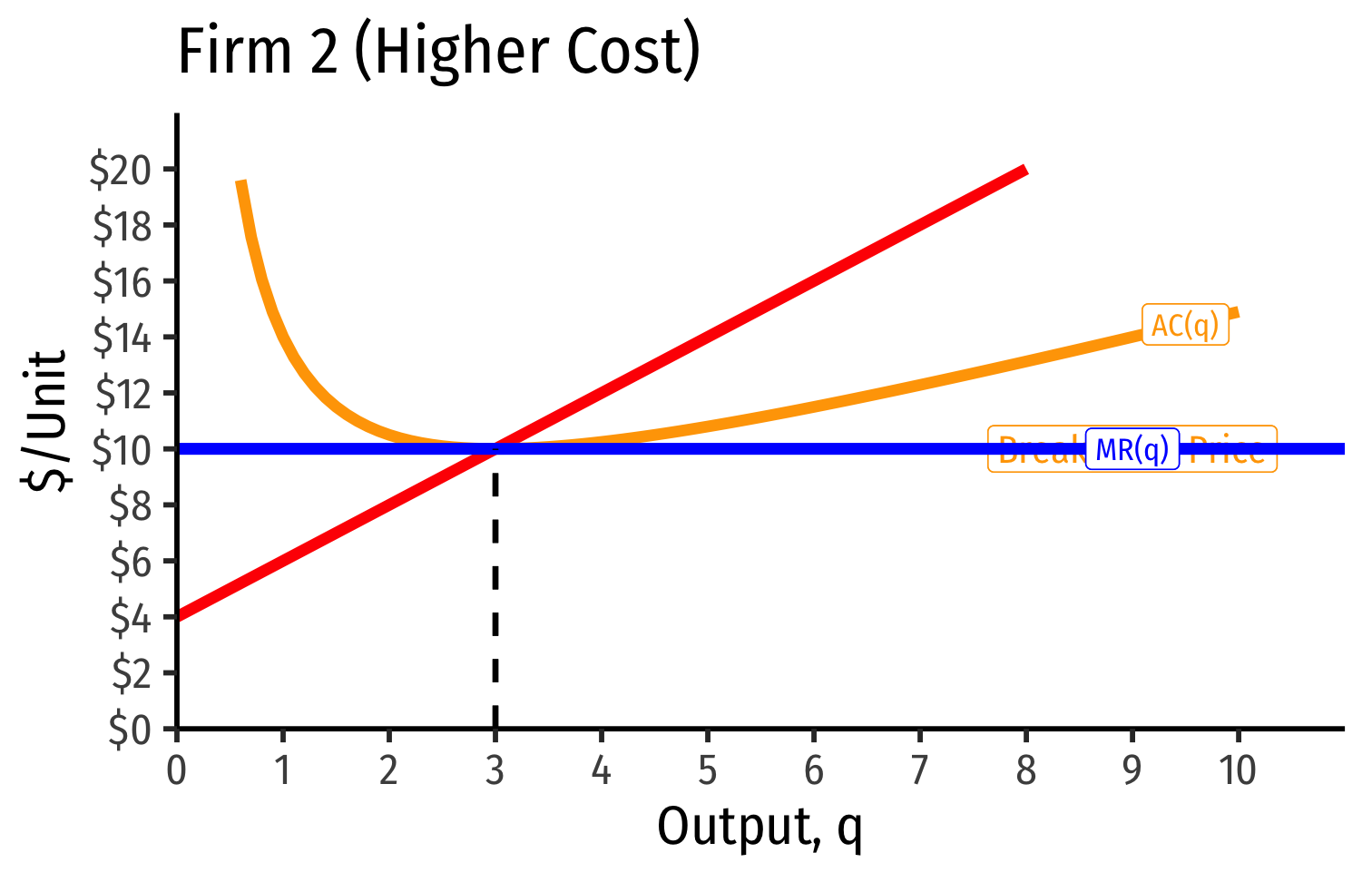
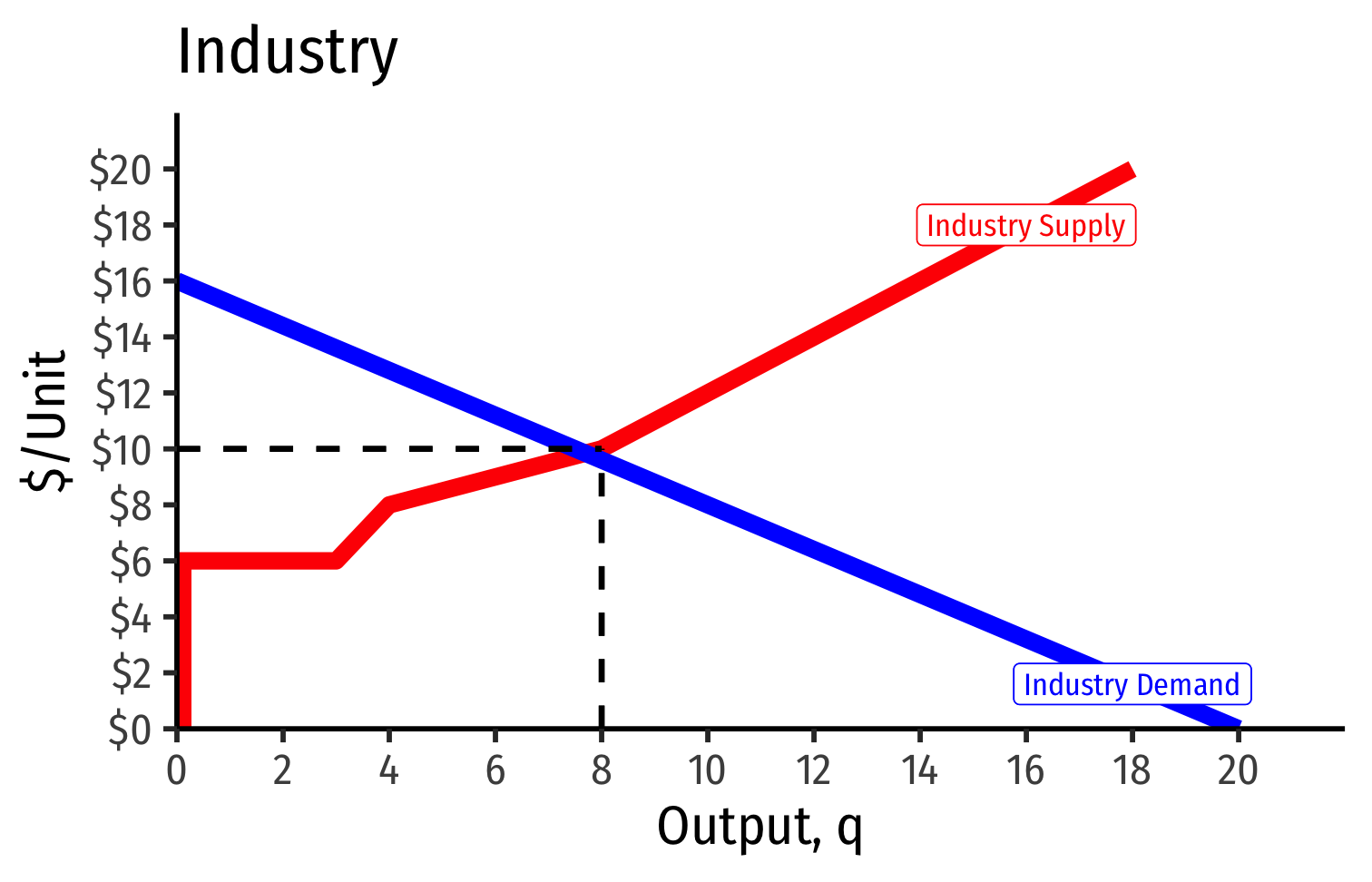
Industry Supply Curves (Different Firms) II



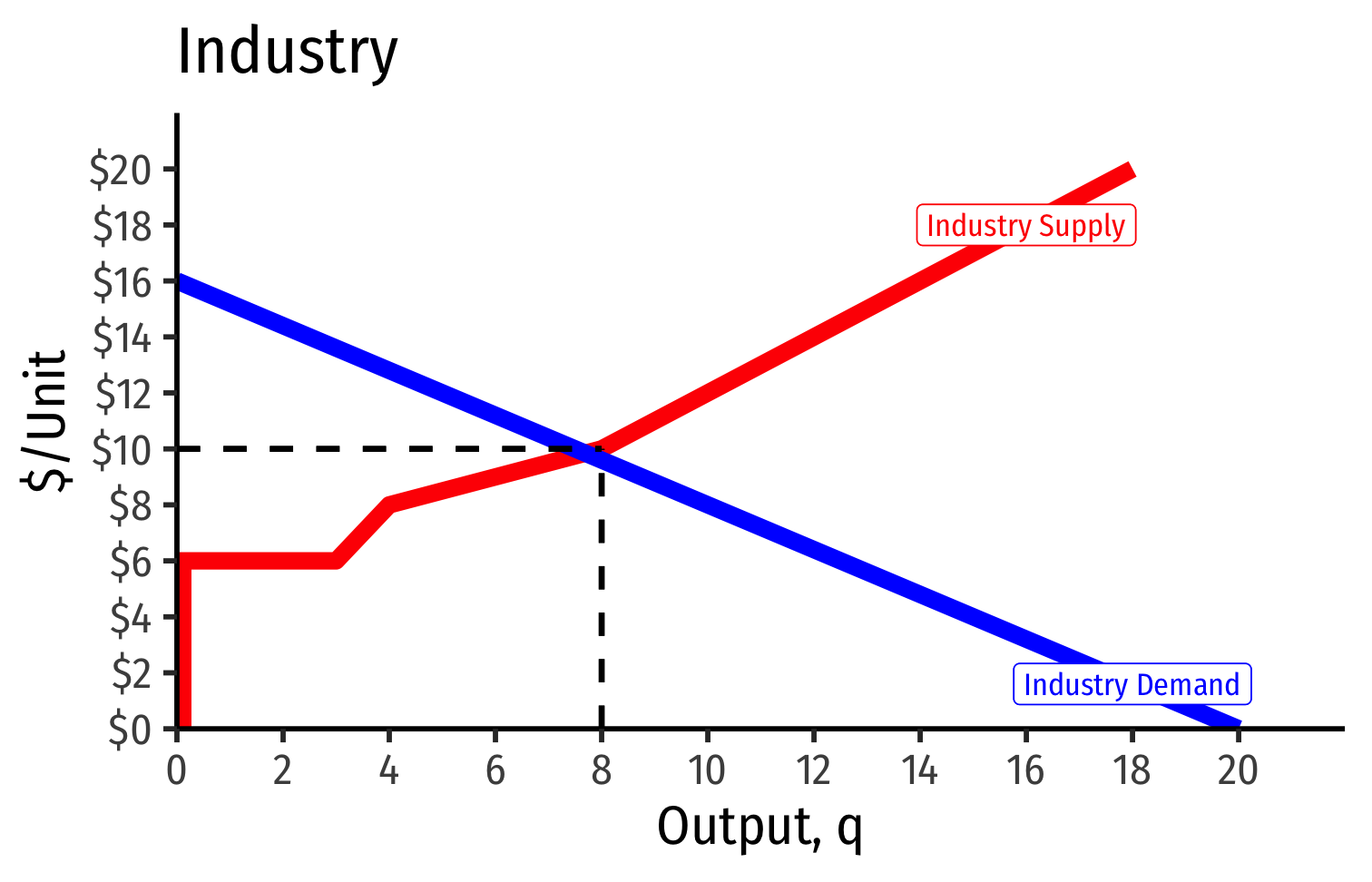
- Industry demand curve (where equal to supply) sets market price, demand for firms
Industry Supply Curves (Different Firms) II



- Industry demand curve (where equal to supply) sets market price, demand for firms
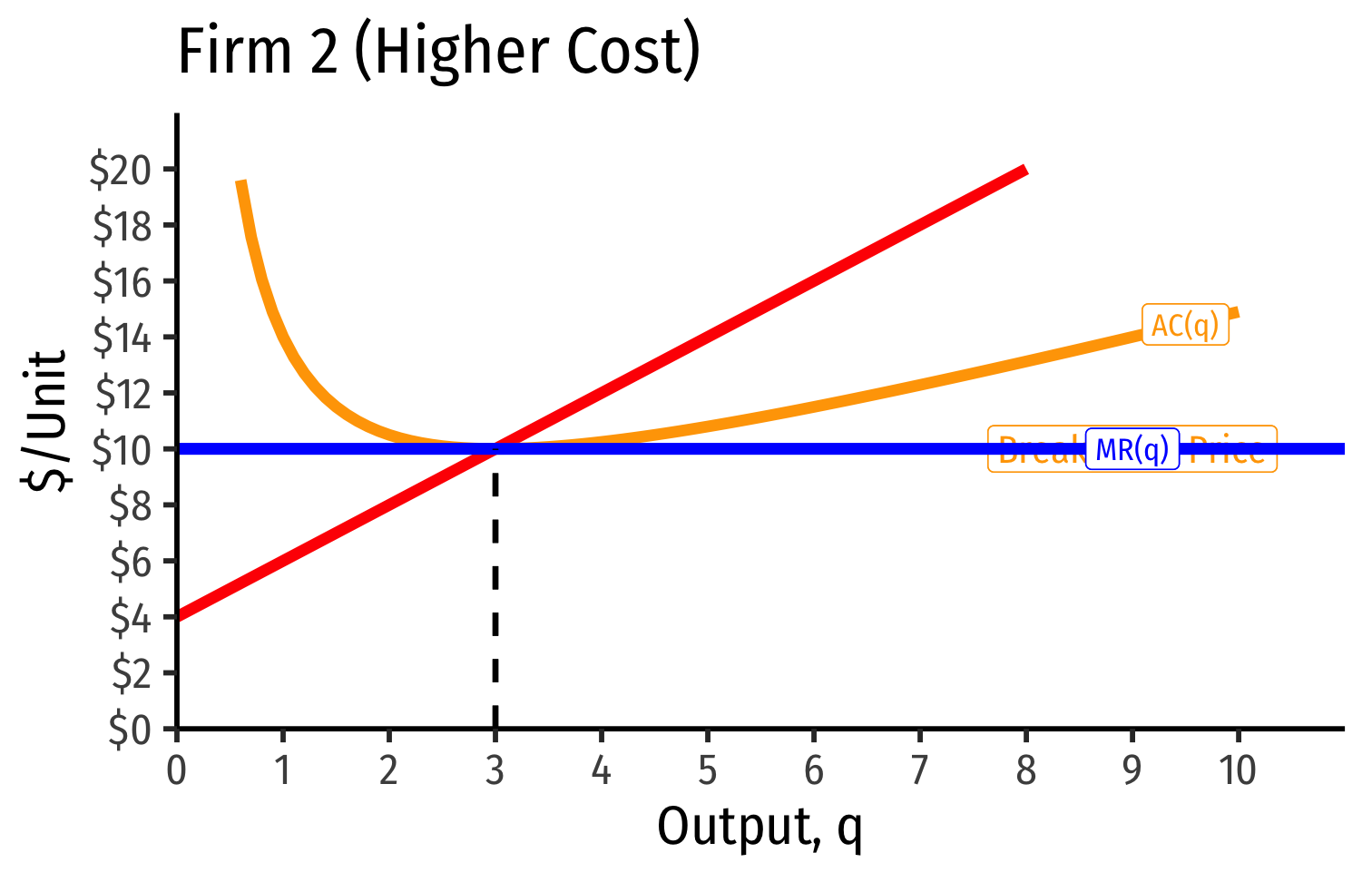
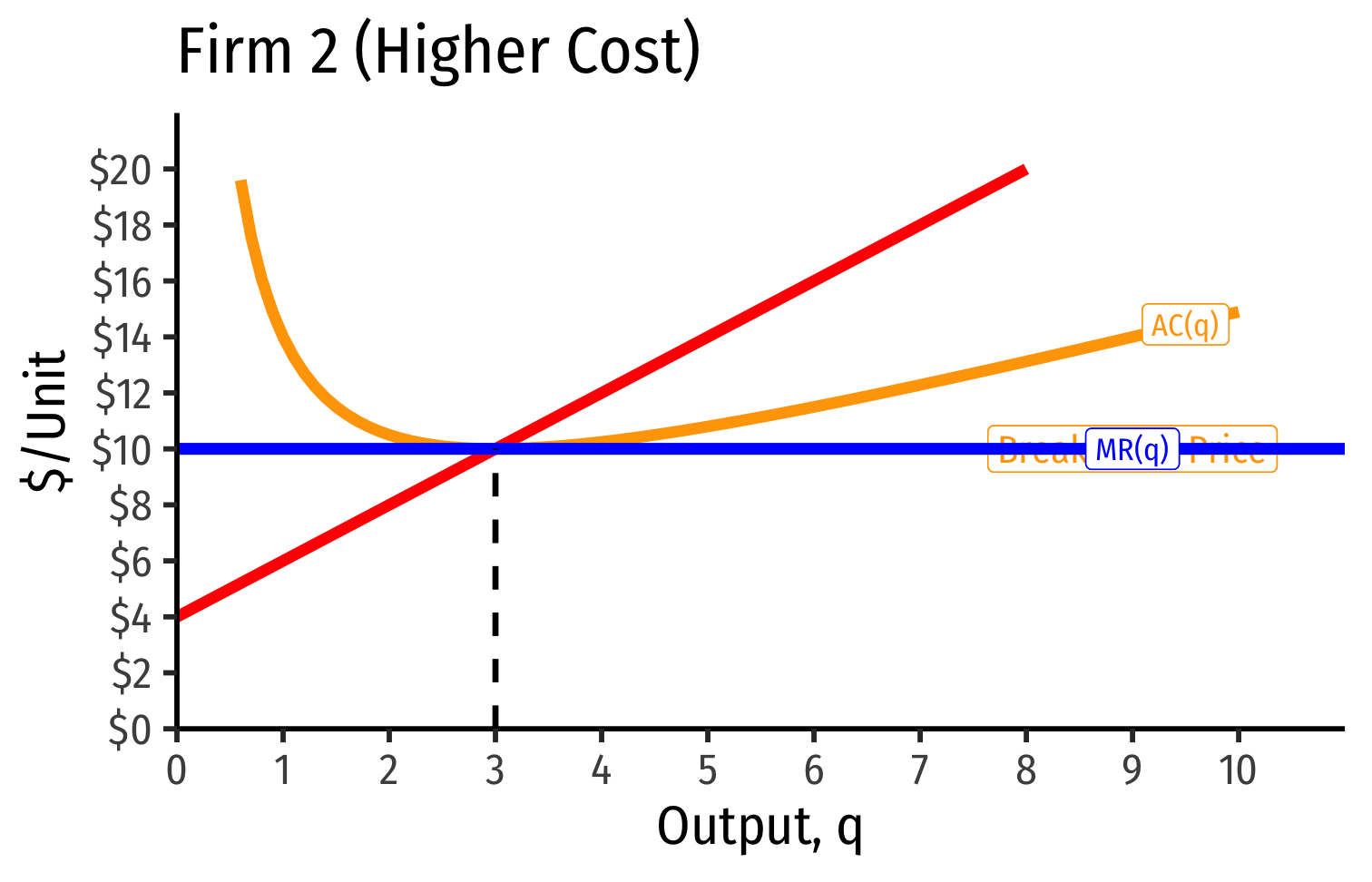
- Long run industry equilibrium: p=AC(q)minp=AC(q)min, π=0π=0 for marginal (highest cost) firm (Firm 2)
Industry Supply Curves (Different Firms) II



- Industry demand curve (where equal to supply) sets market price, demand for firms
- Long run industry equilibrium: p=AC(q)minp=AC(q)min, π=0π=0 for marginal (highest cost) firm (Firm 2)
- Firm 1 (lower cost) appears to be earning profits...(we’ll come back to this)
Economic Rents and Zero Economic Profits I

Long-run equilibrium p=AC(q)minp=AC(q)min of the marginal (higher-cost) firm
A marginal firm cannot profitably enter
- Otherwise, if p>AC(q)p>AC(q) for that firm, would induce more entry into industry!
Economic Rents and Zero Economic Profits I

“Inframarginal” (lower-cost) firms are using resources that earn economic rents
- returns higher than their opportunity cost (what is needed to bring them into this industry)
Economic rents arise from relative differences between resources
Economic Rent

Economic rent: a return or payment for a resource above its normal market return (opportunity cost)
Has no allocative effect on resources, entirely “inframarginal”
A windfall return that resource owners get for free
Sources of Economic Rents

- Some factors are relatively scarce in the whole economy
- (talent, location, secrets, IP, licenses, being first, political favoritism)
Firms Using Resources with Economic Rents

Inframarginal firms that employ these scarce factors gain a short-run profits from having lower costs/higher productivity
...But what will happen to the prices for their scarce factors over time?
Economic Rents Examples


Economic Rents and Zero Economic Profits

In a competitive market, over the long run, profits are dissipated through competition
- Rival firms willing to pay for the scarce factor to gain an advantage
Competition over acquiring the scarce factors pushes up their prices
- i.e. higher costs to firms of using the factor!
Rents are included in the opportunity cost (price) for inputs over long run
- Must pay a factor enough to keep it out of other uses
Economic Rents and Zero Economic Profits

From the firm’s perspective, over the long-run, rents are included in the price (opportunity cost) of the scarce factor
- Must pay a factor enough to keep it out of other uses
Firm does not earn the rents, it raises firm’s costs and squeezes profits to zero!
Economic Rents Reduce Firms’ Profits Over Long Run
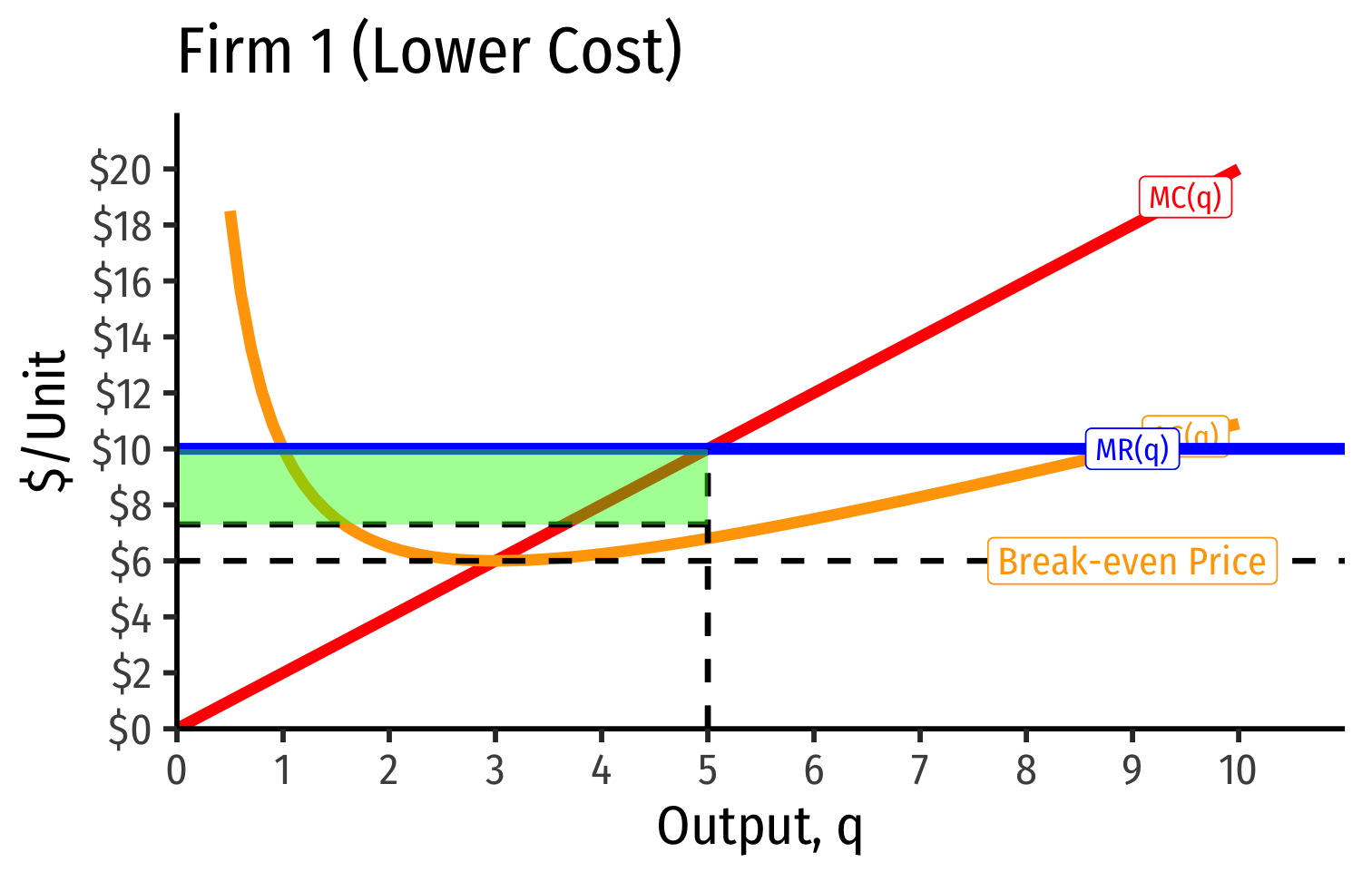
- Short Run: firm that possesses scarce rent-generating factors has lower costs, perhaps short-run profits
Economic Rents Reduce Firms’ Profits Over Long Run
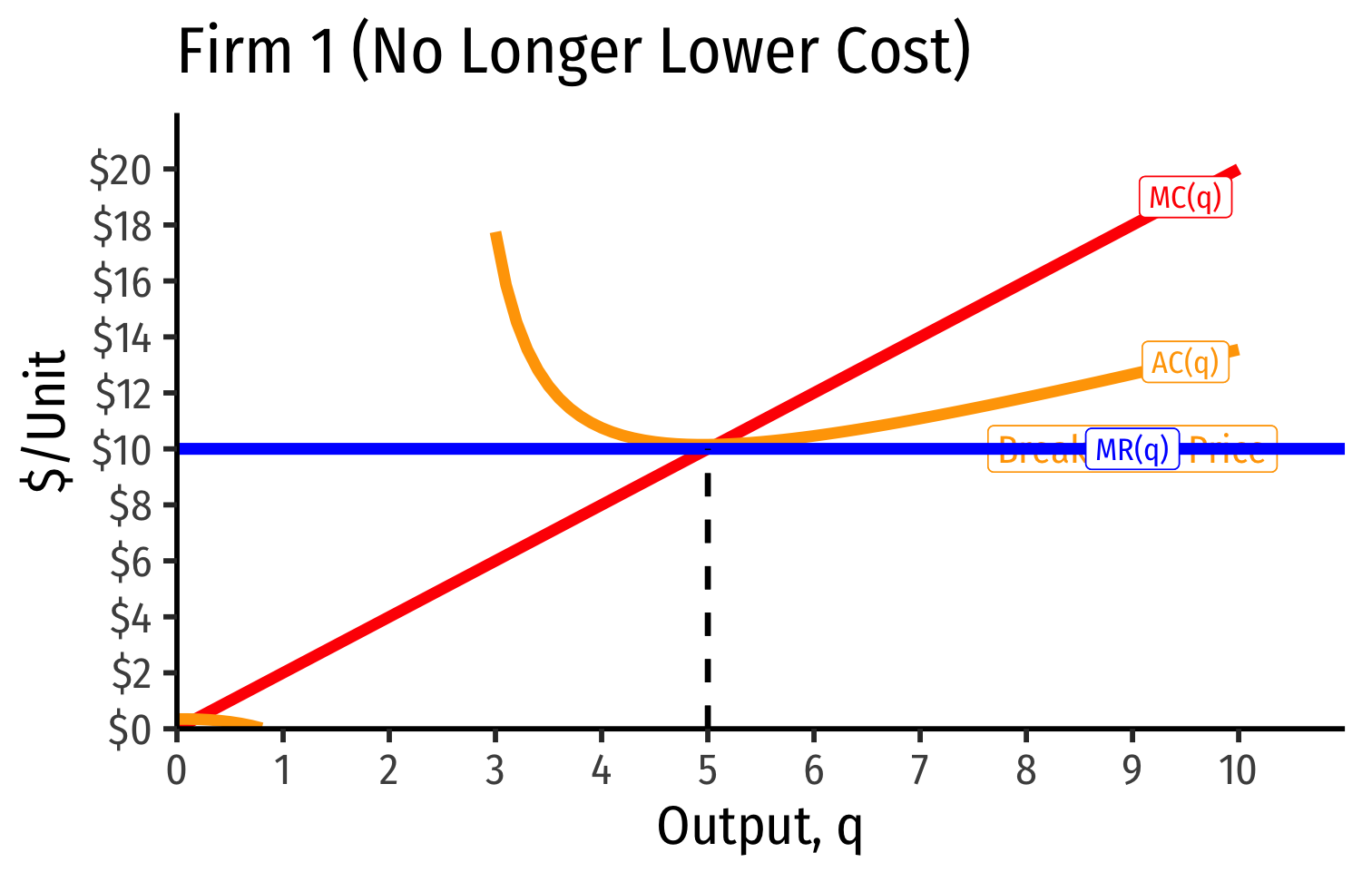
Short Run: firm that possesses scarce rent-generating factors has lower costs, perhaps short-run profits
Long run: competition over those factors pushes up their prices, raising costs to firm, until its profits go to zero as well
- Increase in fixed cost (scarce factor), raising AC(q), which now includes rents (more info in appendix)
Economic Rents Go To Resource Owners

Owners of scarce factors (workers, landowners, inventors, etc) earn the rents as higher income for their services (wages, land rent, interest, royalties, etc).
Often induces competition to supply alternative factors, which may dissipate the rents (to zero)
- More workers invest in becoming talented, try to create new inventions, build new land, etc.
Recall: Accounting vs. Economic Point of View
Recall “economic point of view”:
Producing your product pulls scarce resources out of other productive uses in the economy
Profits attract resources: pulled out of other (less valuable) uses
Losses repel resources: pulled away to other (more valuable) uses
Zero profits keep resources where they are
- Implies society is using resources optimally


Supply Functions
Supply Function
- Supply function relates quantity to price
Example: q=2p−4q=2p−4
- Not graphable (wrong axes)!
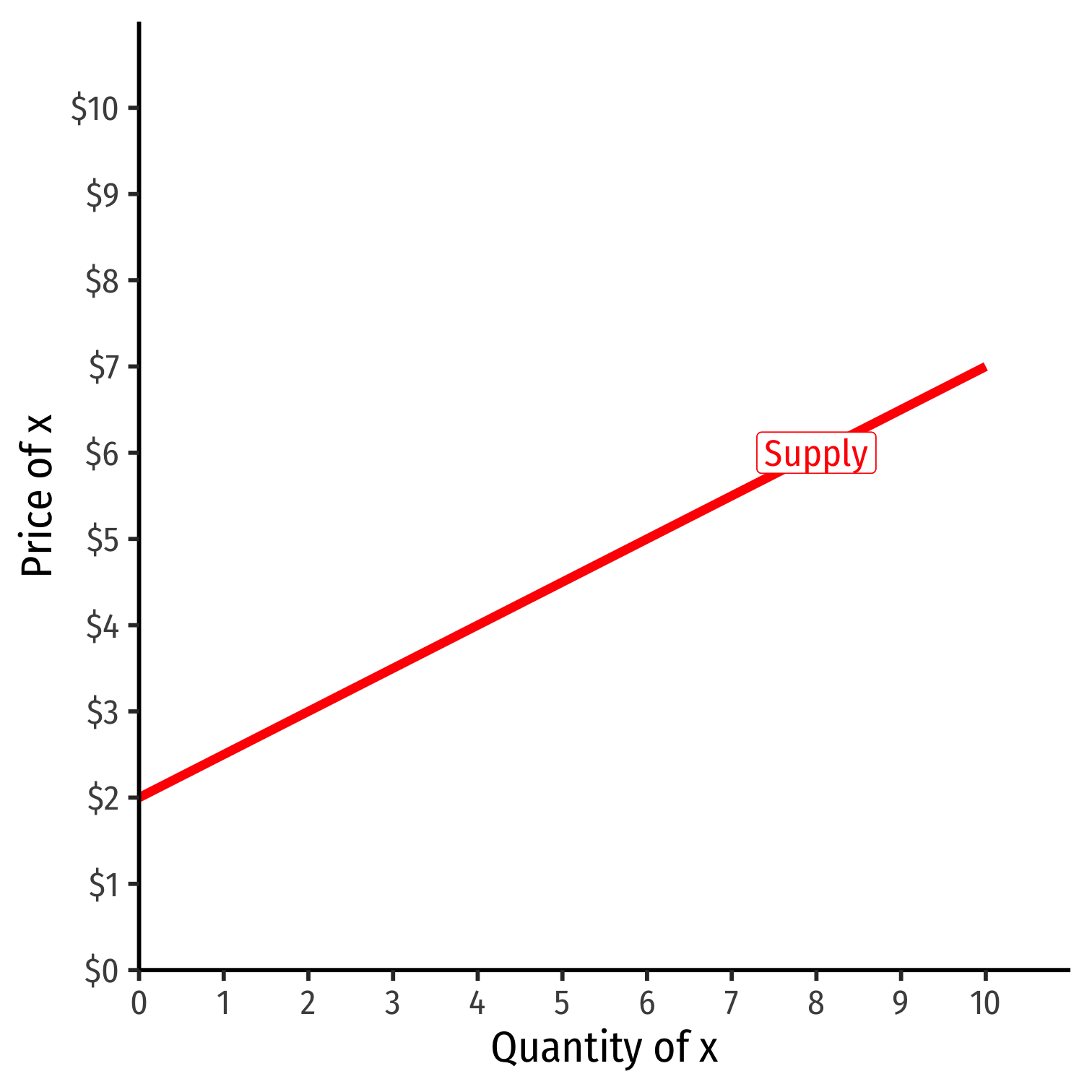
Inverse Supply Function
- Inverse supply function relates price to quantity
- Take supply function, solve for pp
Example: p=2+0.5qp=2+0.5q
- Graphable (price on vertical axis)!
Inverse Supply Function
- Inverse supply function relates price to quantity
- Take supply function, solve for pp
Example: p=2+0.5qp=2+0.5q
- Graphable (price on vertical axis)!
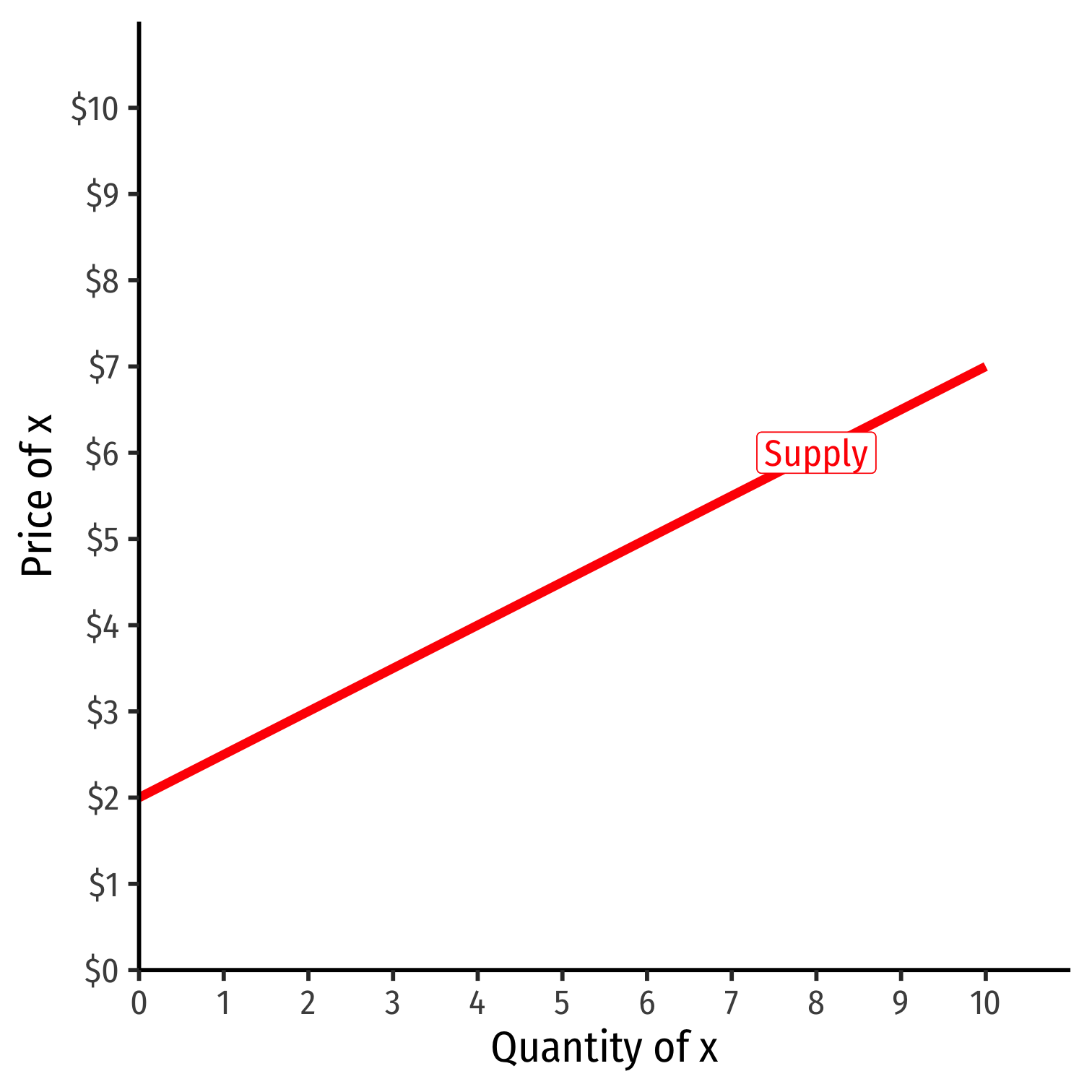
Inverse Supply Function
Example: p=2+0.5qp=2+0.5q
Slope: 0.5
Vertical intercept called the "Choke price": price where qS=0qS=0 ($2), just low enough to discourage any sales
- Consider the shut-down price...
Inverse Supply Function
Read two ways:
Horizontally: at any given price, how many units firm wants to sell
Vertically: at any given quantity, the minimum willingness to accept (WTA) for that quantity
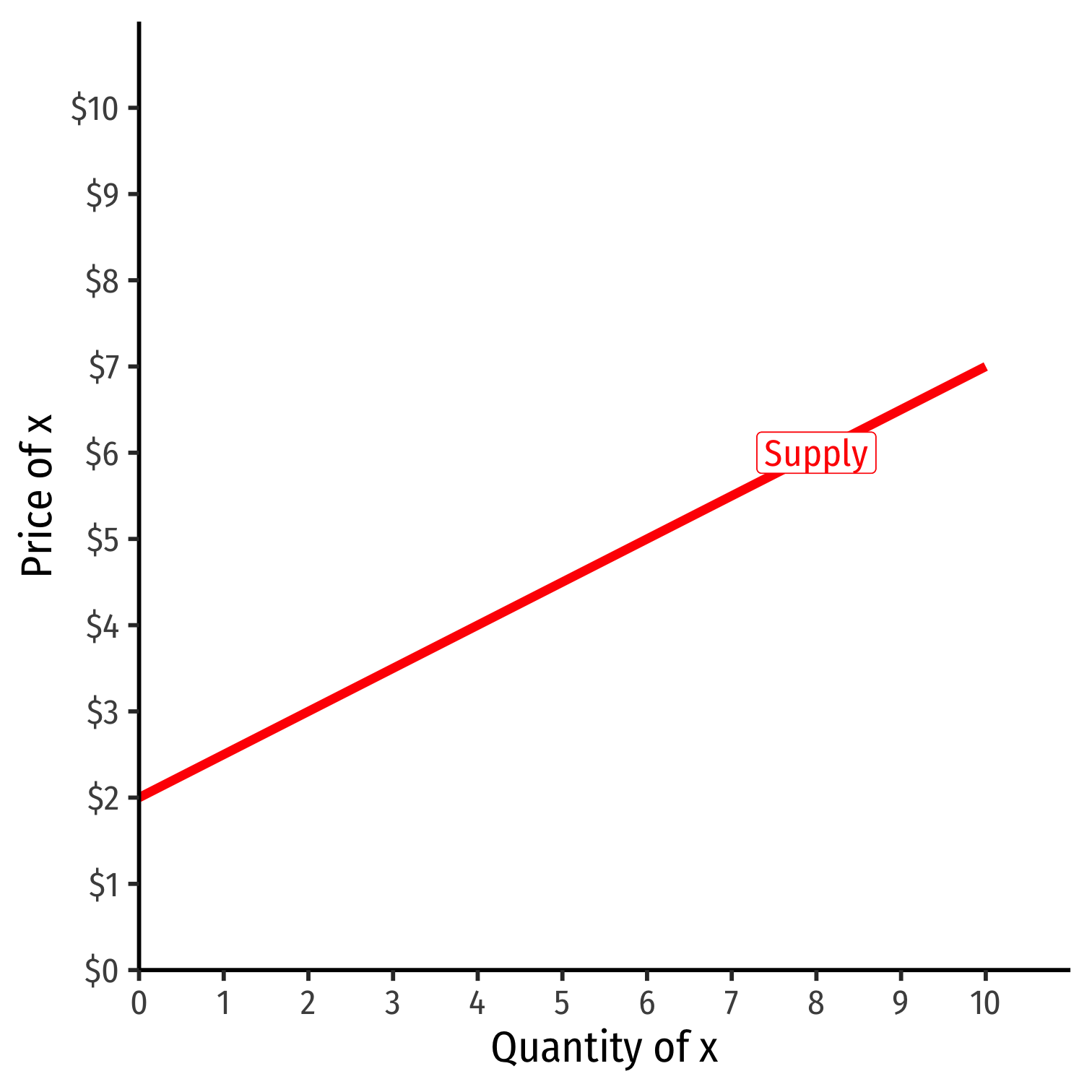
Price Elasiticity of Supply
Price Elasticity of Supply
- Price elasticity of supply measures how much (in %) quantity supplied changes in response to a (1%) change in price
εqS,p=%ΔqS%ΔpεqS,p=%ΔqS%Δp

Price Elasticity of Supply: Elastic vs. Inelastic
εqS,p=%ΔqS%ΔpεqS,p=%ΔqS%Δp
| “Elastic” | “Unit Elastic” | “Inelastic” | |
|---|---|---|---|
| Intuitively: | Large response | Proportionate response | Little response |
| Mathematically: | εqs,p>1εqs,p>1 | εqs,p=1εqs,p=1 | εqs,p<1εqs,p<1 |
| Numerator >> Denominator | Numerator == Denominator | Numerator << Denominator | |
| 1% change in pp causes | More than 1% change in qsqs | Exactly 1% change in qsqs | Less than 1% change in qsqs |
Compare to price elasticity of demand
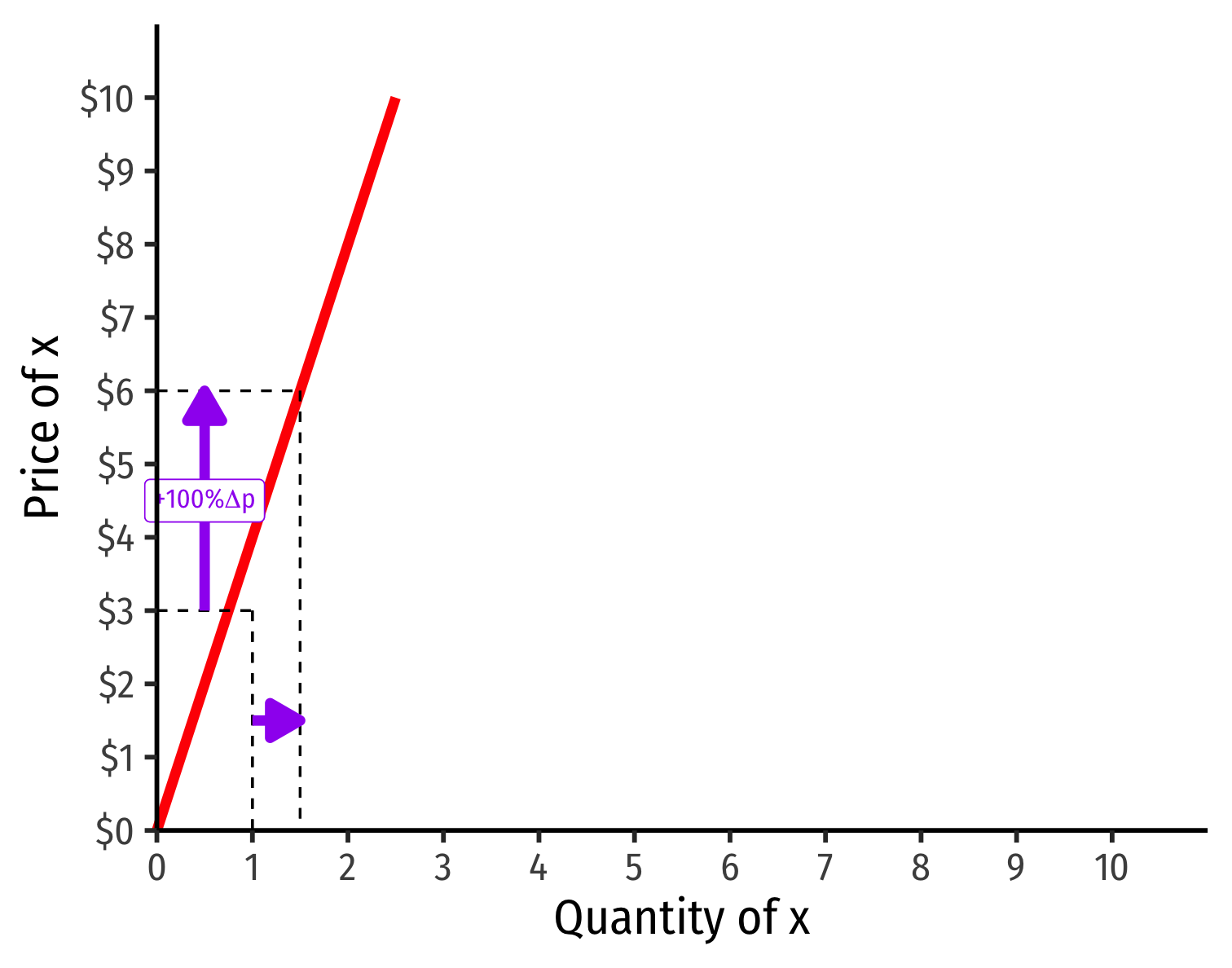
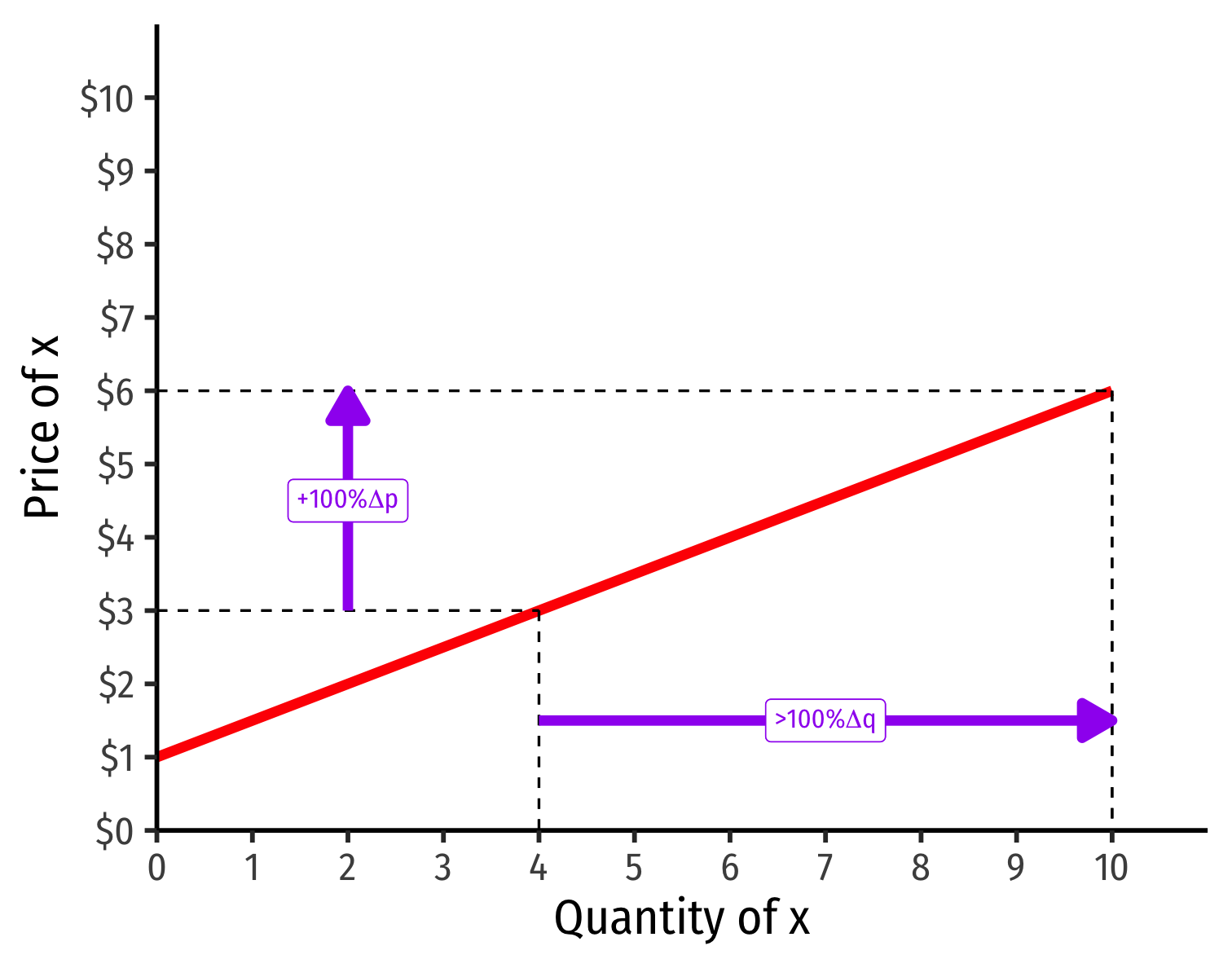
Visualizing Price Elasticity of Supply
An identical 100% price increase on an:
“Inelastic” Supply Curve
“Elastic” Supply Curve
Price Elasticity of Supply Formula
εq,p=1slope×pqεq,p=1slope×pq
First term is the inverse of the slope of the inverse supply curve (that we graph)!
To find the elasticity at any point, we need 3 things:
- The price
- The associated quantity supplied
- The slope of the (inverse) supply curve

Example
Example: The supply of bicycle rentals in a small town is given by:
qS=10p−200qS=10p−200
Find the inverse supply function.
What is the price elasticity of supply at a price of $25.00?
What is the price elasticity of supply at a price of $50.00?
Price Elasticity of Supply Changes Along the Curve
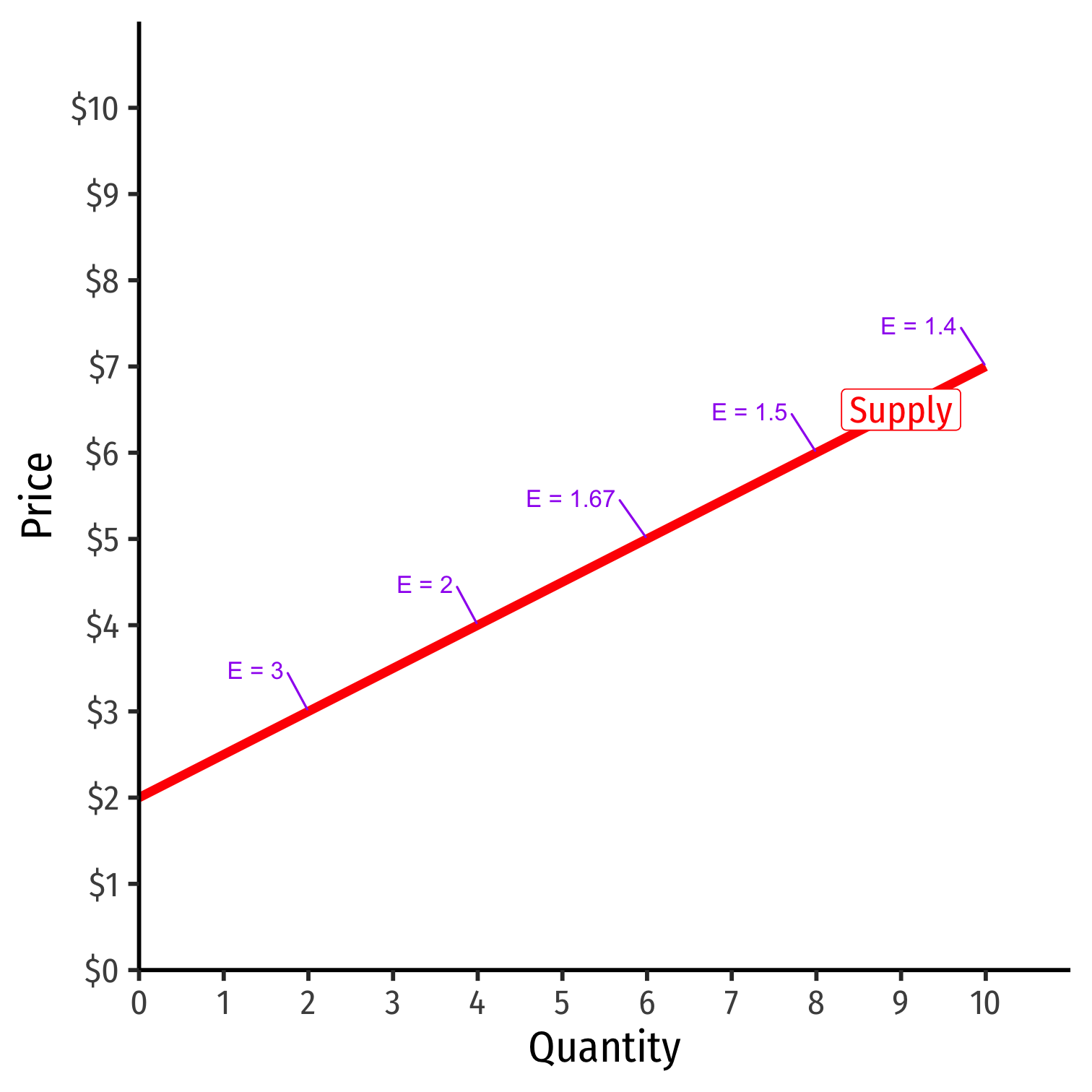
εq,p=1slope×pqεq,p=1slope×pq
Elasticity ≠≠ slope (but they are related)!
Elasticity changes along the supply curve
Often gets less elastic as ↑↑ price (↑(↑ quantity)
- Harder to supply more
Determinants of Price Elasticity of Supply I
What determines how responsive your selling behavior is to a price change?
The faster (slower) costs increase with output ⟹⟹ less (more) elastic supply
- Mining for natural resources vs. automated manufacturing
Smaller (larger) share of market for inputs ⟹⟹ more (less) elastic
- Will your suppliers raise the price much if you buy more?
- How much competition is there in your input markets?

Determinants of Price Elasticity of Supply II
What determines how responsive your selling behavior is to a price change?
- More (less) time to adjust to price changes ⟹⟹ more (less) elastic
- Supply of oil today vs. oil in 10 years

Price Elasticity of Supply: Examples

Source: Washington Post (Oct 2, 2021): “Inside America’s Broken Supply Chain”
Price Elasticity of Supply: Examples